What can we say if this hyperbola and parabola meet at right angles?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let the point of intersection be \((p,q)\). Thus \[\begin{equation} q^2 = 4ap \text{, and } pq=c^2.\label{eq:intersection} \end{equation}\]

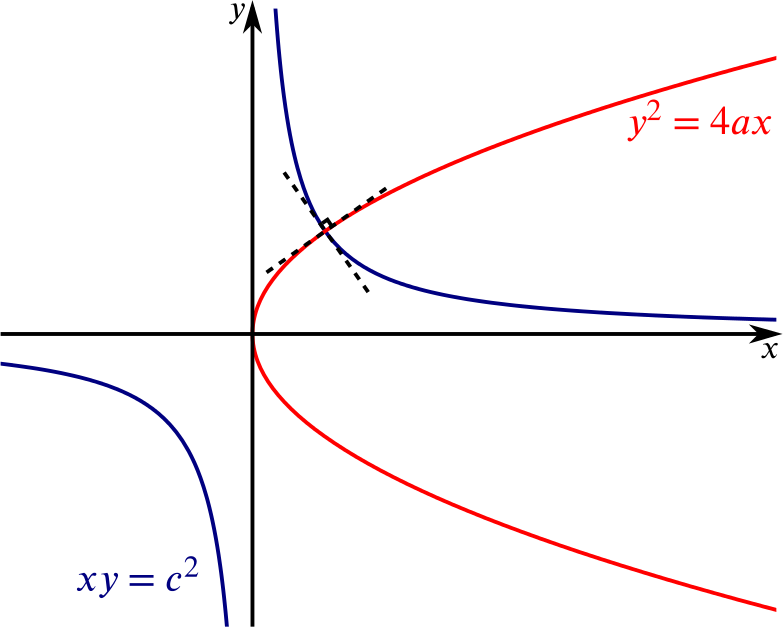
Using implicit differentiation on \(y^2 =4ax\), we have \(2y\dfrac{dy}{dx} = 4a\), so the gradient at \((p,q)\) is \(\dfrac{dy}{dx} = \dfrac{2a}{q}\).

Similarly, differentiating \(xy=c^2\), we have \(y+x\dfrac{dy}{dx} = 0\), so \(\dfrac{dy}{dx}= \dfrac{-y}{x}\), and the gradient at \((p,q)\) is \(\dfrac{-q}{p}\).

Since the curves are at right angles at \((p,q)\), we have \(\dfrac{2a}{q}\times\dfrac{-q}{p}=-1\), which simplifies to \(p = 2a\).

Combining this with \(\eqref{eq:intersection}\) we have \(q^2 = 8a^2\), and since \(p^2q^2=c^4\) we have \((2a)^28a^2 = c^4\), or \(c^4=32a^4\), as required.

The tangent and normal both pass through \((p,q)\) and have gradients \(\dfrac{2a}{q}\) and \(\dfrac{-q}{p}\). So we can write their equations as \[x-p = \dfrac{2a}{q}(y-q),\qquad\text{and}\quad x-p = \dfrac{-q}{p}(y-q) .\]

Let these lines meet the \(x\)-axis at \((x_1,0)\) and \((x_2,0)\). Then we have \[x_1-p = -\dfrac{2a}{q}q,\qquad\text{and}\quad x_2-p = \dfrac{q}{p}q .\]

Subtracting these two and substituting from \(\eqref{eq:intersection}\), \[x_2-x_1 = \frac{q^2}{p}+2a = \frac{4ap}{p}+2a = 6a\] as required.