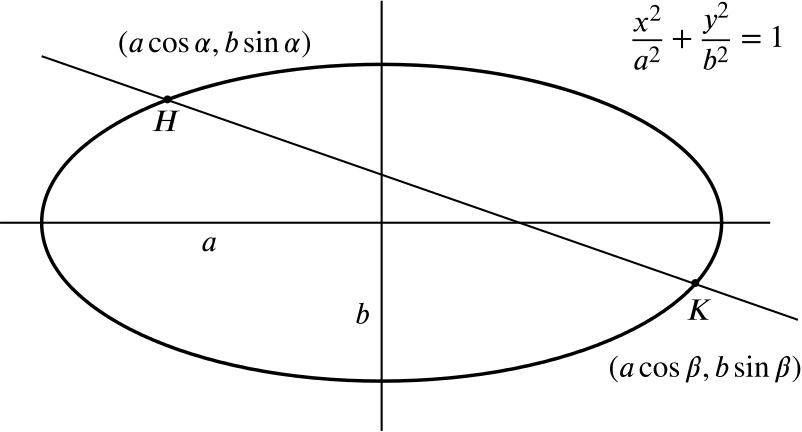
Prove that the equation of the chord of the ellipse \[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\] joining the points \((a\cos\alpha,b\sin\alpha)\) and \((a\cos\beta,b\sin\beta)\) is \[\frac{x}{a}\cos\left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b}\sin\left(\frac{\alpha+\beta}{2}\right)= \cos\left(\frac{\alpha-\beta}{2}\right).\]
The following standard identities will be useful to us:
\[\sin x- \sin y = \sin \dfrac{x-y}{2}\cos \dfrac{x+y}{2}, \cos x -\cos y = -2 \sin \dfrac{x+y}{2} \sin \dfrac{x-y}{2}.\]
The gradient of the chord \(HK\) is \[\frac{b\sin\alpha-b\sin\beta}{a\cos\alpha-a\cos\beta}\] \[=-\dfrac{b}{a} \frac{\sin \dfrac{x-y}{2}\cos \dfrac{x+y}{2}}{\sin \dfrac{x+y}{2} \sin \dfrac{x-y}{2}}\] \[=-\dfrac{b}{a} \frac{\cos \dfrac{x+y}{2}}{\sin \dfrac{x+y}{2}}.\]
Therefore the equation of the line is \[y-b\sin\alpha=-\dfrac{b}{a} \frac{\cos \frac{\alpha+\beta}{2}}{\sin \frac{\alpha+\beta}{2}}(x-a\cos\alpha)\] or \[xb\cos\left(\frac{\alpha+\beta}{2}\right)+ay\sin\left(\frac{\alpha+\beta}{2}\right)= ab \sin \frac{\alpha + \beta}{2}\sin \alpha + ab \cos \frac{\alpha + \beta}{2}\cos \alpha,\] which simplifies to \[\frac{x}{a}\cos\left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b}\sin\left(\frac{\alpha+\beta}{2}\right)= \cos\left(\frac{\alpha-\beta}{2}\right).\]
as required.We can find the equation of the tangent through \(H\) by allowing \(\beta\) to tend to \(\alpha\), giving us \[bx\cos\alpha+a\sin\alpha-ab=0.\]
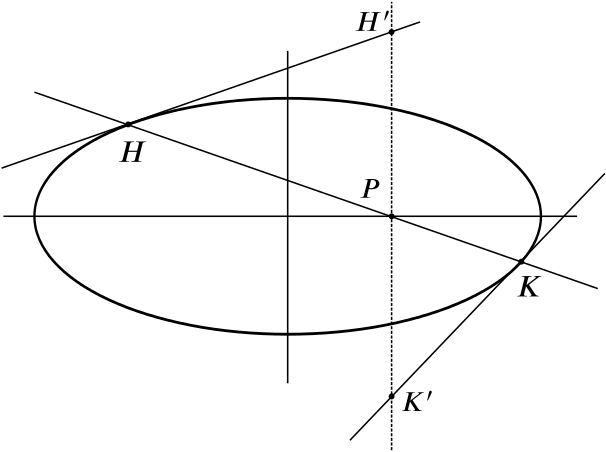
Through a point \(P\) on the major axis of an ellipse a chord \(HK\) is drawn. Prove that the tangents at \(H\) and \(K\) meet the line through \(P\) at right angles to the major axis at points equidistant from \(P\).
We can find the point \(P(x_p,0)\) by substituting \(y=0\) into the equation of the chord found above: \[x_p=a\frac{\cos\left(\frac{\alpha-\beta}{2}\right)}{\cos\left(\frac{\alpha+\beta}{2}\right)}.\]
From our work above, the tangent through \(H\) is \(bx\cos\alpha+a\sin\alpha-ab=0,\) while the equation of the tangent though \(K\) is \(bx\cos\beta+a\sin\beta-ab=0.\)
We are looking to prove that $ PH’ =PK’$, where \(H'\) and \(K'\) are the intersections of the tangents with the line through \(P\).
Let \(H'\) be \((x_p,y_h)\) and \(K'\) be \((x_p,y_k)\). The signs of \(y_h\) and \(y_k\) will always be opposite, since the chord \(HK\) crosses the \(x\)-axis.
Consider the equation \[(bx\cos\alpha+ay\sin\alpha-ab)(bx\cos\beta+ay\sin\beta-ab)=0.\]
This must represent the equation of the pair of straight lines given by the tangent at \(H\) and the tangent at \(K\).
Where does the line \(x = x_p\) cut these lines? At \(H'\) and \(K'\). So let’s substitute \(x_p\) for \(x\) in this equation, giving
\[(bx_p\cos\alpha+ay\sin\alpha-ab)(bx_p\cos\beta+ay\sin\beta-ab)=0.\]
This is a quadratic in \(y\), say \(Ay^2+By+C=0\). Its roots must be \(y_h\) and \(y_k\), and the sum of these roots is \(-\dfrac{B}{A}\). Thus
\[y_h+y_k = -\dfrac{a\sin\beta(bx_p\cos\alpha-ab)+a\sin\alpha(bx_p\cos\beta-ab)}{a^2\sin\alpha\sin\beta}\] \[=-b\dfrac{x_p\sin(\alpha+\beta)-a(\sin\alpha+\sin\beta)}{a\sin\alpha\sin\beta}\] \[=-b\dfrac{\dfrac{\cos\dfrac{\alpha-\beta}{2}}{\cos\dfrac{\alpha + \beta}{2}}2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha+\beta}{2}-(\sin\alpha+\sin\beta)}{\sin\alpha\sin\beta}\] \[=-b\dfrac{2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}-(\sin\alpha+\sin\beta)}{\sin\alpha\sin\beta}\]The following standard identity is now useful: \[2\sin x\cos y = \sin (x+y)+\sin(x-y) \implies 2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2} = \sin\alpha+\sin\beta.\]
And so we have that \(y_h+y_k =0\), and the lengths \(PH'\) and \(PK'\) are equal, as required.

