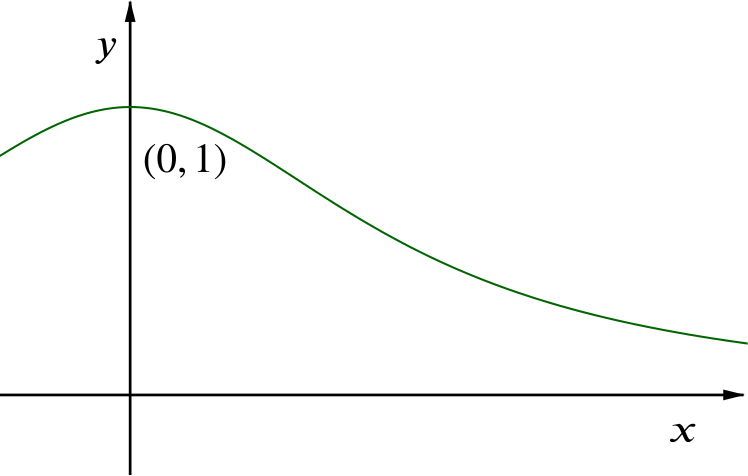
Give a sketch of the curve \(y=\dfrac{1}{1+x^2}\), for \(x \geq 0\).
In order to sketch the curve, we notice:
We have that \(y\ge0\) for all \(x\ge 0\).
At \(x=0\), we have \(y=1\), so it passes through the point \((0,1)\).
As \(x\) gets large, \(y\) gets small. This means that \(y\to 0\) as \(x\to \infty\).
Taking the derivative, we find that \[\frac{dy}{dx}=-\frac{2x}{(1+x^2)^2},\] so we have \(\dfrac{dy}{dx}=0\) at \(x=0\), so \((0,1)\) is a stationary point of the curve.
For \(x>0\), we have that \(\dfrac{dy}{dx}<0\), so the curve is decreasing as \(x\) increases.
Using these facts, we can now sketch the curve.
Find the equation of the line that intersects the curve at \(x=0\) and is tangent to the curve at some point with \(x>0\). Prove that there are no further intersections between the line and the curve. Draw the line on your sketch.
Let us draw the sketch of the curve with the tangent immediately.
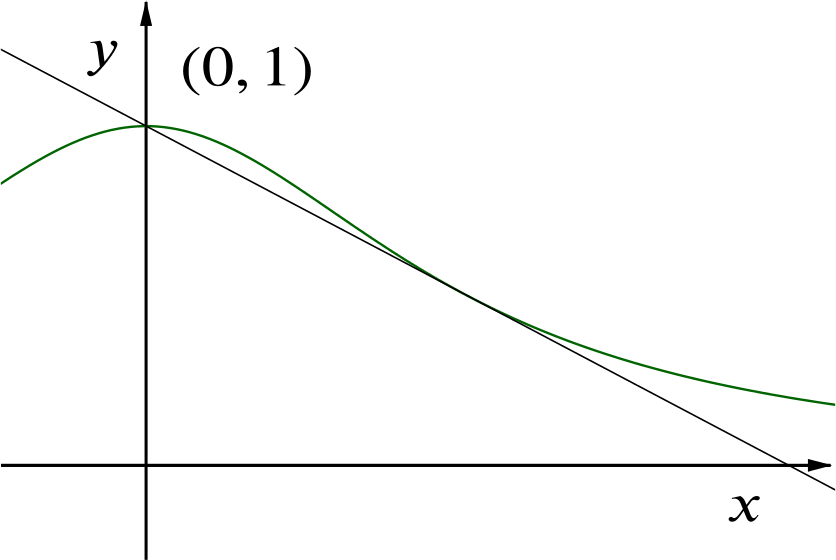
The straight line we want intersects the curve at \((0,1)\), that is, its \(y\)-intercept is \(1\). So it has an equation of the form \(y=mx+1\).
Solving \(y=mx+1\) simultaneously with \(y=\dfrac{1}{1+x^2}\) gives a cubic equation, so there can be at most three crossing points (one of which will be repeated if the line is tangent to the curve).
Approach 1: Using the discriminant
Solving these equations simultaneously, we have \[mx+1=\frac{1}{1+x^2},\] so \[(mx+1)(1+x^2)=1.\] Expanding the brackets gives \[mx^3+x^2+mx+1=1\] so \[\begin{equation} x(mx^2+x+m)=0.\label{eq:intersect} \end{equation}\]This has the root \(x=0\) (as the line intersects the curve at \(x=0\)) and the quadratic \(mx^2+x+m=0\) has a double root if the discriminant of the quadratic is zero, so \[1-4m^2=0,\] yielding \(m=\pm\dfrac{1}{2}\). We must have \(m=-\dfrac{1}{2}\) and so \(x=1\) at the point of tangency. The line therefore has equation \(y=1-\dfrac{1}{2}x\).
Approach 2: Using calculus
The tangent line will be of the form \(y = mx +1\). Let the point where the line touches the curve be \((p,q)\).
We know therefore that
- \((p,q)\) is on the curve
- \((p,q)\) is on the line
- the gradient of the curve equals that of the line at \((p,q)\).
This tells us that \(q = \dfrac{1}{1+p^2}\), \(q=mp+1\), and \(\dfrac{-2p}{(1+p^2)^2} = m\) (using the gradient function we derived earlier).
Thus \(\dfrac{1}{1+p^2}=\dfrac{-2p}{(1+p^2)^2}p+1,\) which yields \(p=1\) (since \(p > 0\)), and hence \(q = \dfrac{1}{2}, m = -\dfrac{1}{2}\).
The line therefore has equation \(y=1-\dfrac{1}{2}x\).
By considering the area under the curve for \(0\le x\le 1\), show that \(\pi>3\).
\(\left[\text{Note:} \displaystyle\int_0^1\dfrac{1}{1+x^2} \:dx = \dfrac{\pi}{4}.\right]\)
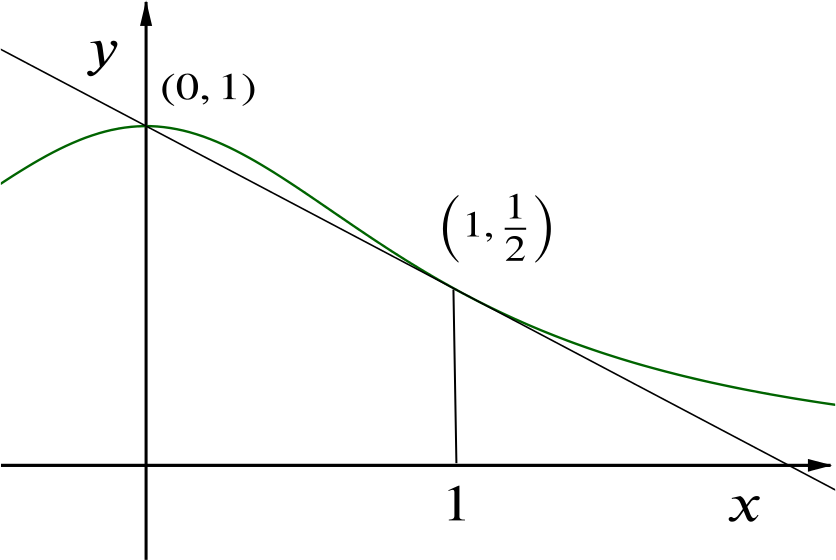
The area under the curve for \(0\le x\le 1\) is strictly greater than that of the trapezium bounded by the lines \(x=0\), \(x=1\), \(y=0\) and \(y=1-\dfrac{1}{2}x\).
So \[\int_0^1 \frac{1}{1+x^2} dx> \frac{1}{2}\left(1+\frac{1}{2}\right).\] By the note given in the question, we therefore know \[\frac{\pi}{4}>\frac{3}{4},\] that is, \[\pi>3.\]
Show also, by considering the volume formed by rotating the curve about the \(y\) axis, that \(\ln 2>2/3\).
The equation of the curve \(y = \dfrac{1}{1+x^2}\) can be rearranged to the form \(x^2=\dfrac{1}{y}-1\).
When \(x=0\), \(y=1\) and when \(x=1\), \(y=1/2\).
The volume of revolution of the curve about the \(y\) axis is therefore given by \[\begin{align*} \pi\int x^2 dy &= \pi\int_\frac{1}{2}^1 \frac{1}{y}-1 dy\\ &= \pi \left[\ln y-y\right]^1_{1/2}\\ &= \pi \left[(\ln 1-1)-\left(\ln \frac{1}{2}-\frac{1}{2}\right)\right]\\ &= \pi (\ln 2-\frac{1}{2}) \end{align*}\]The equation of the line \(y=1-\dfrac{x}{2}\) can be rearranged to the form \(x=2-2y\).
The volume of the shape given by rotating the line \(y=1-\dfrac{x}{2}\) about the \(y\) axis is \[\begin{align*} \pi\int x^2 dy &= \pi\int_\frac{1}{2}^1 (2-2y)^2 dy\\ &= \pi\int_\frac{1}{2}^1 4-8y+4y^2 dy\\ &= \pi \left[4y-4y^2+\frac{4}{3}y^3\right]^1_\frac{1}{2}\\ &= \pi \left[\left(4-4+\frac{4}{3}\right)-\left(2-1+\frac{1}{6}\right)\right]\\ &= \frac{1}{6}\pi \end{align*}\]Since volume of the shape of the rotated curve is greater than that of the shape of the rotated line, we have \[\pi\left(\ln 2 - \frac{1}{2}\right) > \frac{1}{6}\pi,\] that is, \[\ln 2>\frac{2}{3}.\]

