When is the volume of this pyramid a maximum?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The volume \(V\) of a right square pyramid is given by the equation \[ V = \frac{1}{3} \times \text{area of the base} \times \text{height}. \] As the square base comprises four rods, each of length \(x\), the area of the base is \(x^2\). For the height, consider the following image.

We wish to calculate \(h\). By Pythagoras’s theorem, we have \[\begin{align*} h^2 + \left( \frac{x}{\sqrt{2}} \right)^2 = (a - x)^2 &\implies h^2 = a^2 - 2ax + x^2 - \frac{x^2}{2} \\ &\implies h = \sqrt{a^2 - 2ax + \frac{x^2}{2}}. \end{align*}\] Thus, we have that \[\begin{align*} V &= \frac{1}{3} \times x^2 \times \sqrt{a^2 - 2ax + \frac{x^2}{2}} \\ &= \frac{1}{3} \sqrt{ a^2x^4 - 2ax^5 + \frac{x^6}{2} }. \end{align*}\] By the chain rule, \[\begin{align*} \frac{dV}{dx} &= \frac{1}{6} \left( a^2x^4 - 2ax^5 + \frac{x^6}{2} \right)^{-1/2} \times \left( 4a^2 x^3 - 10ax^4 + 3x^5 \right) \\ &= \frac{x^3(3x^2 - 10ax + 4a^2)}{6\sqrt{a^2x^4 - 2ax^5 + \frac{x^6}{2}}} \\ &= \frac{x(3x^2 - 10ax + 4a^2)}{6\sqrt{a^2 - 2ax + \frac{x^2}{2}}}. \end{align*}\]

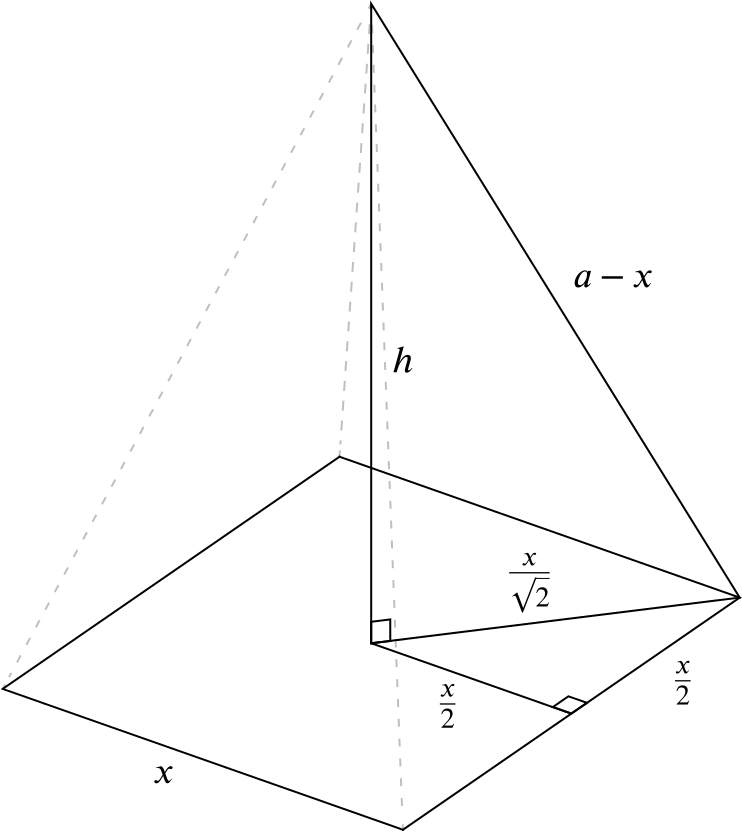
So we can see that, \(\dfrac{dV}{dx} = 0\) when \(x = 0\) or \(3x^2 - 10ax + 4a^2 = 0\).

From the quadratic formula, \[ 3x^2 - 10ax + 4a^2 = 0 \iff x = \frac{10a \pm \sqrt{100a^2 - 48a^2}}{6} = \frac{10 \pm \sqrt{52}}{6} a = \frac{5 \pm \sqrt{13}}{3} a. \]

The smaller of these roots is \(x=\dfrac{5 - \sqrt{13}}{3} a\).

In order to form a real pyramid, \(x\) must be between \(0\) and \(a\). Also, the sloping diagonal, \(a-x\), must be longer than the semi-diagonal of the base, \(\dfrac{x}{\sqrt{2}}\).

Since \(5>\sqrt{13}\), we know that \(x\) is positive. We also require \[\begin{align*} a-x &> \frac{x}{\sqrt{2}} \\ \iff\quad x\left(1+\frac{1}{\sqrt{2}}\right) &< a \\ \iff\quad x &< \left(2-\sqrt{2}\right)a \end{align*}\]

Comparing these surd expressions directly is tricky, so let’s use a calculator to check. \[\dfrac{5 - \sqrt{13}}{3} \approx 0.465 \quad\text{and}\quad 2-\sqrt{2} \approx 0.586\] so the diagonal condition is satisfied and we do have a real pyramid.

As \(x \to 0\), the square base goes to a point and the volume of the pyramid shrinks to zero.

As \(x \to \left(2-\sqrt{2}\right)a\), the sloping diagonal becomes the same length as the semi-diagonal of the base. The height and therefore the volume of the pyramid shrinks to zero.

In between these values, a real pyramid exists and \(V\) is positive.

We know that in this range, we have a single stationary point, which must therefore be a maximum.