A piece of thin wire of length \(L\) binds together two cylindrical welding rods, of radii \(R\) and \(r\), by passing all the way around them both.

Find \(L\) in terms of \(R\) and \(r\).
We can see from the picture that the wire is made up of two arcs of circles joined by two straight lines.
Let’s find the lengths of the straight lines first.
The straight part of the wire runs along two lines that are tangent to both circles. Drawing in radii of the circles that are perpendicular to this tangent line and the straight line joining the centres of the two circles, we have the following picture:
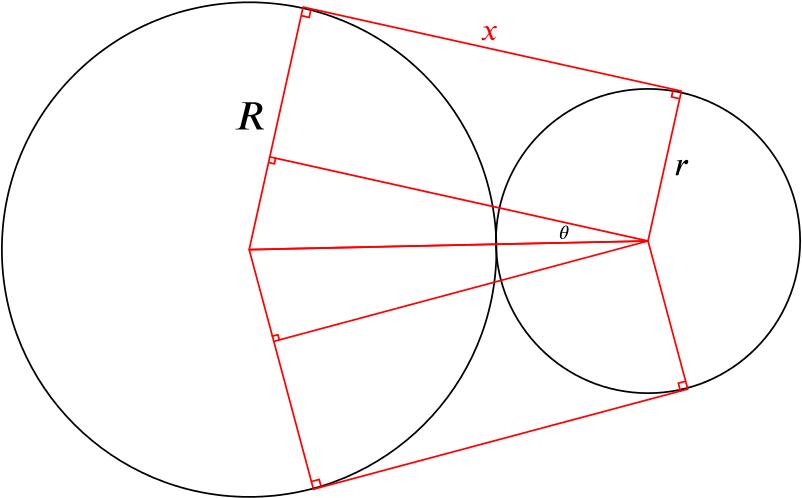
We have also drawn in an extra line of the same length of those we want to find, but further down, creating a triangle.
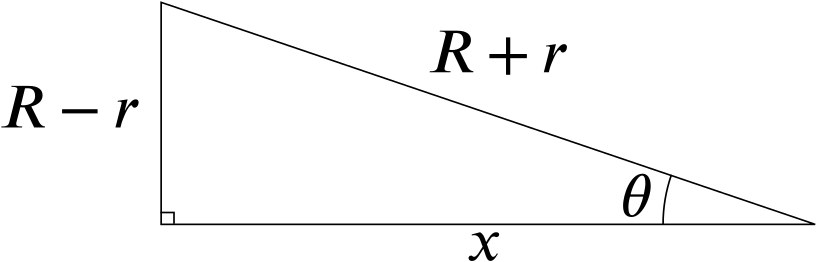
We can use this to find the length of \(x\), as well as the value of \(\theta\). Notice that the bottom triangle is a reflection of the top triangle, so that both line segments have the same length. (And we are assuming that \(R>r\).)
Using Pythagoras’s Theorem, we find that \[x=\sqrt{(R+r)^2-(R-r)^2}=\sqrt{4Rr}=2\sqrt{Rr},\] and using trigonometry we have that \[\sin\theta=\frac{R-r}{R+r},\] and so \[ \theta=\sin^{-1}\left(\frac{R-r}{R+r}\right). \]
Now let’s find the lengths of the arcs.
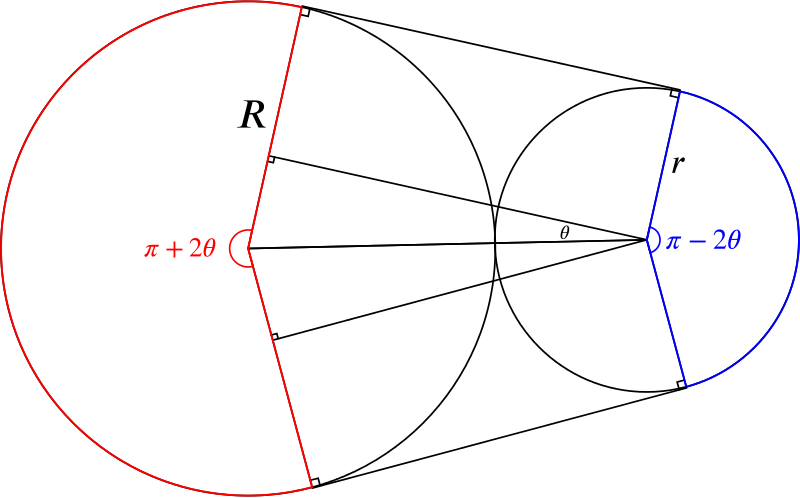
We know the angles of the arcs from our earlier drawing. The red angle (on the left) is the whole circle without two times the third (unmarked) angle in our triangle (which we know must be \(\pi/2-\theta\)), and so the red angle must be \[2\pi-2\left(\frac{\pi}{2}-\theta\right)=\pi+2\theta.\]
The blue angle (on the right) is the whole circle minus two times \(\theta\) minus two right angles, and so must be \[2\pi-2\theta-2\frac{\pi}{2}=\pi-2\theta.\]
So the length of the red (left) arc is \[\frac{\pi+2\theta}{2\pi}2\pi R=\pi R+2\theta R=\pi R +2 R \sin^{-1}\left(\frac{R-r}{R+r}\right),\] and the blue (right) arc has length \[\frac{\pi-2\theta}{2\pi}2\pi r=\pi r-2\theta r= \pi r- 2r \sin^{-1}\left(\frac{R-r}{R+r}\right).\]
So the total length of the wire is \[2\{\text{length of straight line}\}+\{\text{length of blue arc}\}+\{\text{length of red arc}\},\] which is \[4\sqrt{Rr}+\pi(R+r)+2(R-r)\sin^{-1}\left(\frac{R-r}{R+r}\right).\]

