Can we find the equations of two circles that touch another?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let’s call this circle \(D\). Firstly, we rewrite the equation of \(D\) in the form \((x-a)^2+(y-b)^2=r^2\), so that we can easily work out its centre and radius.

We have \[\begin{align*} &x^2+y^2+4x-8y-80=0\\ \iff\quad& (x+2)^2 - 4 + (y-4)^2-16 - 80 =0\\ \iff\quad& (x+2)^2 + (y-4)^2 = 100. \end{align*}\]

\(D\) has centre \((-2,4)\) and radius \(10\). This means that a point \(Q\) lies inside \(D\) if and only if the distance between \(Q\) and the point \((-2,4)\) is less than \(10\).

Let \(d\) be the distance between \((-9,-3)\) and \((-2,4)\). Then \[\begin{align*} d &= \sqrt{(-9-(-2))^2+(-3-4)^2}\\ &= \sqrt{(-7)^2+(-7)^2}\\ &= \sqrt{49+49}\\ &= \sqrt{98} \end{align*}\]

Now \(\sqrt{98} < 10\), so the distance between P and \((-2,4)\) is less than \(10\), and \(P\) lies inside \(D\).

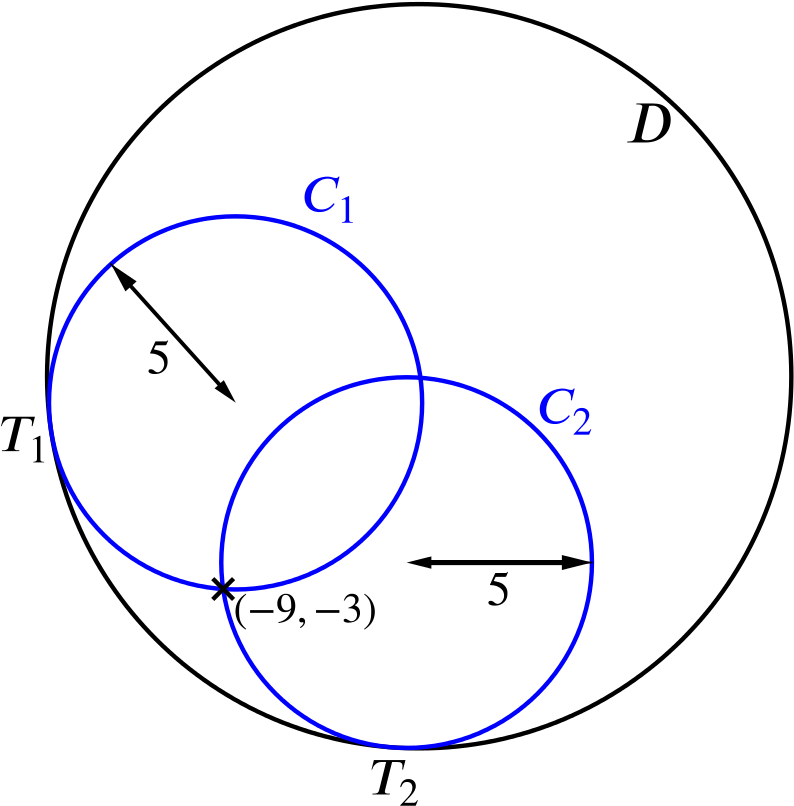
The normal to the circle \(C_1\) at \(T_1\) is also normal to \(D\).

It must go through the centre of \(C_1\), but it must go through the centre of \(D\) too.

Now \(D\) has radius \(10\), and \(C_1\) has diameter \(10\), so we can deduce \(C_1\), and similarly \(C_2\), goes through \((-2,4)\), the centre of \(D\).

Now suppose one of the smaller circles \(C\) has centre \((a,b)\).

The circle \(C\) passes through \((-9,-3)\), so the distance between \((a,b)\) and \((-9,-3)\) is \(5\). So \[(a+9)^2 + (b+3)^2 = 25,\] by Pythagoras’ theorem.

But also \(C\) passes through \((-2,4)\), so the distance between \((a,b)\) and \((-2,4)\) is \(5\). So \[(a+2)^2 + (b-4)^2 = 25,\] by Pythagoras’ theorem.

So we have the two equations \[ a^2+b^2+18a+6b+65=0\] and \[a^2+b^2+4a-8b-5=0.\]

Subtracting these gives \(14a+14b+70=0\), so \[70=-14a-14b\] and \[b=-5-a.\]

Substituting this into \((a+9)^2+(b+3)^2=25\) gives us \[a^2+18a+81+4+4a+a^2=25,\] that is, \[a^2+11a+30=0.\]

This quadratic factorises into \((a+5)(a+6)=0\), so \(a = -5\) or \(a=-6\).

Substituting these values into \(b=-5-a\), we get two possibilities for \((a,b)\), \((-5,0)\) and \((-6,1)\).

It’s easy to check that these points are viable ones for the centre of \(C\) (they do satisfy both equations).

So as the circles have radius \(5\), we get that the equations for these two circles are \[(x+5)^2+y^2=25,\] and \[(x+6)^2+(y-1)^2=25.\]