Find the equation of the circle through the points \(A(2,0)\), \(B(8,0)\), and \(C(10,4)\)…
Given any three points that do not lie on a straight line, there is a unique circle passing through these three points, whose centre is the circumcentre of the triangle.
The circumcentre can be found at the intersection of the perpendicular bisectors of the three sides.
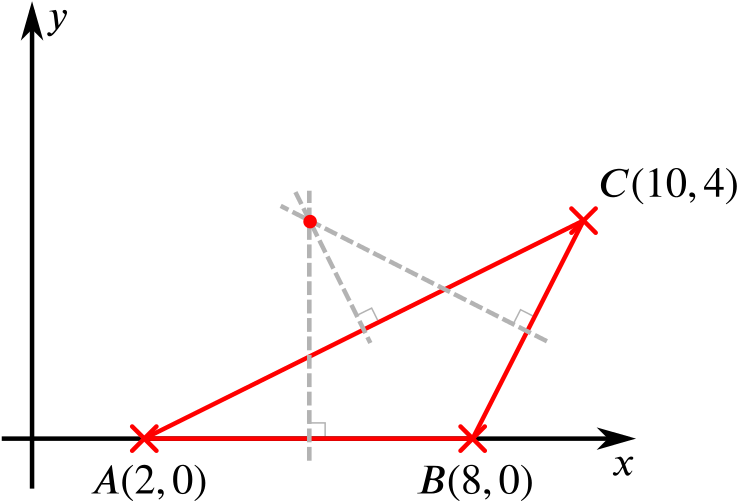

Our three points are \(A=(2,0)\), \(B=(8,0)\), and \(C=(10,4)\).
The line segment between \((2,0)\) and \((8,0)\) is part of the \(x\)-axis, with midpoint \(\left(\dfrac{2+8}{2},\dfrac{0+0}{2}\right)=(5,0)\).
So the perpendicular bisector of the side \(AB\) is the line \(x=5\).
The line segment between \((8,0)\) and \((10,4)\) has gradient \(\dfrac{4}{2}=2\) and midpoint \(\left(\dfrac{8+10}{2},\dfrac{0+4}{2}\right)=(9,2)\).
So the perpendicular bisector of the side \(BC\) is the line with gradient \(-\dfrac{1}{2}\) and passing through the point \((9,2)\).
Substituting this information into the general equation for a line \(y=mx+c\), we find that the perpendicular bisector of the side \(BC\) is the line \(y=-\dfrac{1}{2}x+\dfrac{13}{2}\).
The perpendicular bisector of side \(CA\), which turns out to be the line \(y=-2x+14\), also goes through the circumcentre.
Substituting \(x=5\) into \(y=-\dfrac{1}{2}x + \dfrac{13}{2}\), we get \(y=4\).
So these two perpendicular bisectors intersect at the point \((5,4)\), making this the circumcentre.
Now we can find the radius of the circle—simply find the distance between the centre and one of the points given.
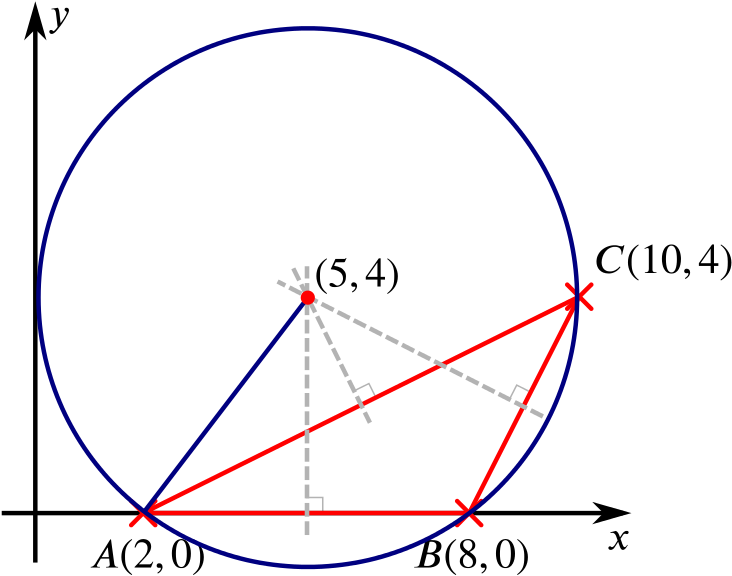
The distance between \(A=(2,0)\) and \((5,4)\) is \(\sqrt{(2-5)^2+(0-4)^2}=\sqrt{25}=5\).
So the circle passing through these three points has centre \((5,4)\) and radius \(5\). This means that it has equation \[(x-5)^2 + (y-4)^2 = 25.\]
An alternative method might argue that we know that \(P\), the centre of the circle, lies on \(x = 5\), so let’s say \(P\) is \((5,p)\).
We also know that \(PB=PC\); this equation enables us to find \(p\), and the rest follows.
… and prove that it touches the \(y\)-axis.
The centre is at (5,4) and the radius is 5, so the circle must touch the y-axis.
Without the use of tables [or calculators] or measurement, find the equation of the other tangent to this circle from the origin.
Any line passing through the origin that is not the \(y\)-axis must have equation \(y=mx\) for some real number \(m\).
We want to find an \(m\) such that \(y=mx\) and \((x-5)^2+(y-4)^2=25\) intersect at exactly one point.
Substituting \(y=mx\) into \((x-5)^2+(y-4)^2=25\) and expanding, we get a quadratic equation in \(x\): \[\begin{align*} &(x-5)^2 + (mx-4)^2 = 25\\ \iff\quad& x^2 - 10x + 25 + m^2x^2 - 8mx + 16 = 25\\ \iff\quad& (m^2 +1)x^2 + (-10 - 8m)x+16 = 0. \end{align*}\]For \(y=mx\) to be a tangent to the circle, this quadratic equation must have only one root, that is, its discriminant must be zero.
The discriminant of the quadratic equation \(ax^2+bx+c = 0\) is \(b^2-4ac\).
The equation has a repeated root if, and only if, the discriminant is zero.
So \(y=-\dfrac{9}{40}x\) is the equation of this tangent.
Note that in general we would expect to have two solutions for \(m\) from \(b^2=4ac\).
When the origin \(O\) is outside the circle, there are exactly two tangents to the circle from \(O\).
Here, however, one of our tangents is the \(y\)-axis, that has infinite gradient.
We could see the equation \(100+160m+64m^2-64m^2-64=0\) as having one solution for \(m\) that is infinite.

