How much of this log is below the surface?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

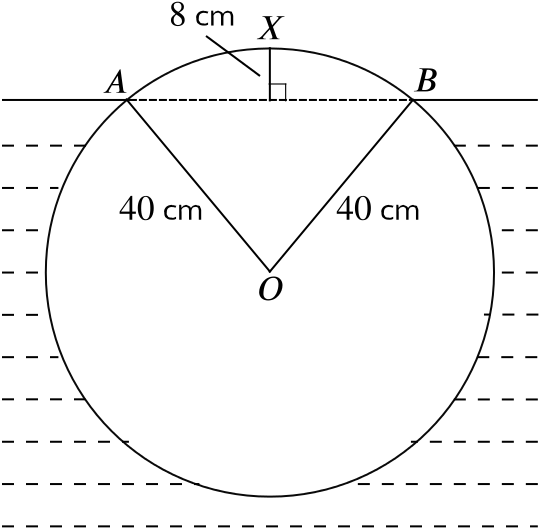
The figure shows the circular cross-section of a uniform log of radius \(\quantity{40}{cm}\) floating in water. The points \(A\) and \(B\) are on the surface and the highest point \(X\) is \(\quantity{8}{cm}\) above the surface.

Show that \(\widehat{AOB}\) is approximately \(1.29\) radians.

Calculate

1. the length of the arc \(AXB\),
2. the area of the cross-section below the surface,
3. the percentage of the volume of the log below the surface.