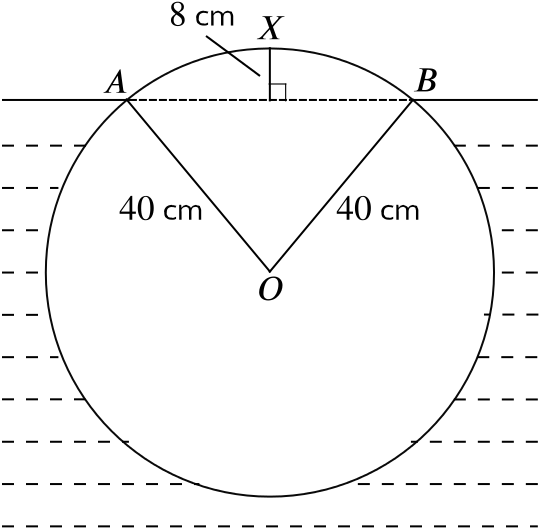
The figure shows the circular cross-section of a uniform log of radius \(\quantity{40}{cm}\) floating in water. The points \(A\) and \(B\) are on the surface and the highest point \(X\) is \(\quantity{8}{cm}\) above the surface.
Show that \(\widehat{AOB}\) is approximately \(1.29\) radians.
Let \(M\) be the point on \(AB\) vertically below \(X\). The length \(OX\) is \(40\) and \(MX\) is \(8\), so \(OM\) is \(\quantity{32}{cm}\).
We’ll compute the angle \(\alpha\), shown here, using its cosine.

We find \[\alpha = \cos^{-1}\left(\frac{32}{40}\right) \approx 0.6435... \text{ radians.}\]
Since the angle \(\widehat{AOB}\) is \(2 \alpha\), we have \(\widehat{AOB} \approx 1.2870... = 1.29\) radians (3sf).
Calculate
- the length of the arc \(AXB\),
The length of the arc is \(s = r\theta\). In our case, \(s \approx 40 \times 1.287 = \quantity{51.5}{cm}\) (3sf).
- the area of the cross-section below the surface,
Let’s call the area of the cross-section below the surface \(S\). We can calculate it as the sum of the triangle \(OAB\) and the major sector \(OAB\).
The area of the triangle is \(\frac{1}{2}a b \sin C = \frac{1}{2} 40^2\sin1.287 \approx 768.0\).
The area of the sector is \(\frac{1}{2}r^2\theta = \frac{1}{2} 40^2(2\pi-1.287) \approx 3997.0\).
So we have \(S\approx768.0+3997.0 = 4765.0 = \quantity{4770}{cm^2}\) (3sf).
- the percentage of the volume of the log below the surface.
The percentage of the volume of the log below the surface is the same as the percentage of the area of the cross-section below the surface.
This is \(\dfrac{4765.0}{\pi 40^2}\times100 \approx 94.80 = 94.8\%\) (3sf).

