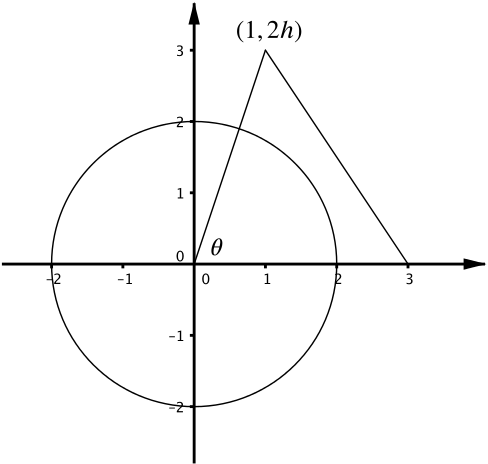
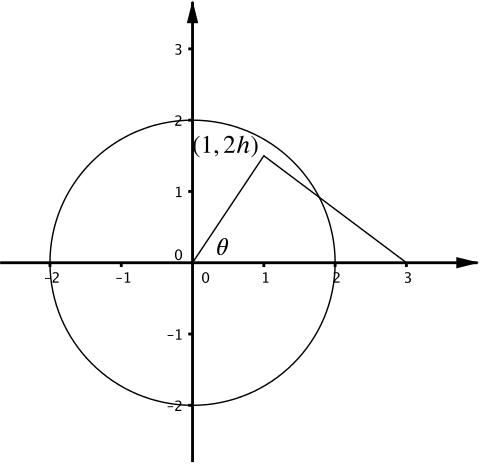
The three corners of a triangle \(T\) are \((0,0), (1, 2h), (3,0)\), where \(h > 0\). The circle \(C\) has equation \(x^2 + y^2 = 4\). The angle of the triangle at the origin is denoted as \(\theta\). The circle and triangle are drawn in the diagram above for different values of \(h\).
- Express \(\tan \theta\) in terms of \(h\).
- Show that the point \((1, 2h)\) lies inside \(C\) when \(h < \sqrt{3}/2\).
- Find the equation of the line connecting \((3,0)\) and \((1,2h)\). Show that this line is tangential to the circle \(C\) when \(h = 2/\sqrt{5}\).
- Suppose now that \(h > 2/\sqrt{5}\). Find the area of the region inside both \(C\) and \(T\) in terms of \(\theta\).
- Now let \(h = 6/7\). Show that the point \((8/5,6/5)\) lies on both the line (from part (iii)) and the circle \(C\).
Hence show that the area of the region inside both \(C\) and \(T\) equals
\[\dfrac{27}{35}+2\alpha,\]
where \(\alpha\) is an angle whose tangent, \(\tan \alpha\), you should determine.
You may use the fact that the area of a triangle with corners \((0,0), (a,b), (c,d)\) is \(\dfrac{1}{2}\vert ad-bc\vert\).

