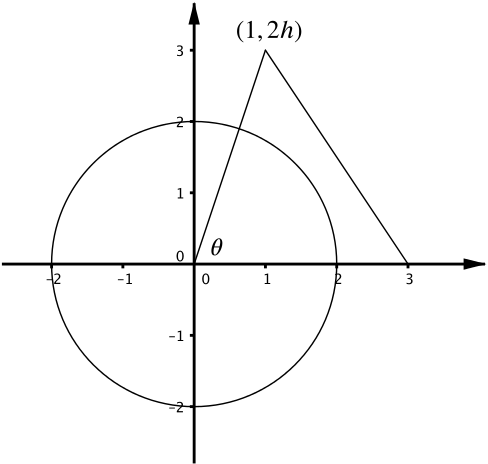
The three corners of a triangle \(T\) are \((0,0), (1, 2h), (3,0)\), where \(h > 0\). The circle \(C\) has equation \(x^2 + y^2 = 4\). The angle of the triangle at the origin is denoted as \(\theta\). The circle and triangle are drawn in the diagram above for different values of \(h\).
- Express \(\tan \theta\) in terms of \(h\).
If we construct a triangle at the point \((1,2h)\) we can see that \(\tan \theta = 2h\).
- Show that the point \((1, 2h)\) lies inside \(C\) when \(h < \sqrt{3}/2\).
The critical point, when \((1,2h)\) lies on the circle, gives us a right-angled triangle with sides \(1, 2h\) and hypotenuse \(2\).
Using Pythagoras here gives \(h = \dfrac{\sqrt{3}}{2}\), and so the point \((1,2h)\) is inside the circle if and only if \(h < \dfrac{\sqrt{3}}{2}\).
- Find the equation of the line connecting \((3,0)\) and \((1,2h)\). Show that this line is tangential to the circle \(C\) when \(h = 2/\sqrt{5}\).
The equation of the line is \(\dfrac{y-0}{x-3}= \dfrac{2h-0}{1-3}\), or \(y = -hx+3h\).
Substituting in to \(x^2 + y^2 = 4\) gives \(x^2 + (-hx+3h)^2 = 4\), and multiplying out gives us \(x^2(1+h^2) +x(-6h^2) +(9h^2-4)=0\).
The discriminant here for this quadratic in \(x\) is
\[36h^4-4(1+h^2)(9h^2-4) = -20h^2+16.\]
This is zero if and only if \(h = \dfrac{2}{\sqrt{5}}\), and so for this value of \(h\), our line is tangential to the circle \(C\), since it intersects \(C\) in one point only.
Alternatively we can substitute \(h = \dfrac{2}{\sqrt{5}}\) into \(x^2 + (-hx+3h)^2 = 4\) and observe we get one possible value for \(x\).
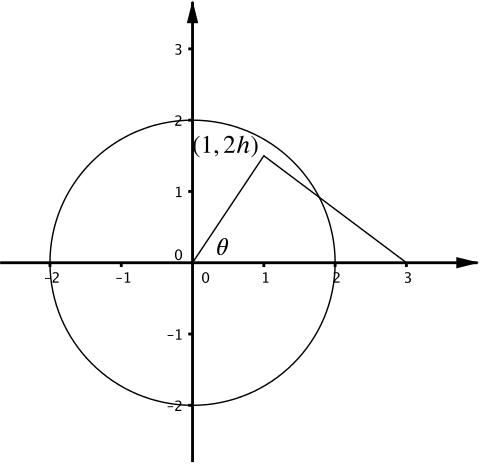
- Suppose now that \(h > 2/\sqrt{5}\). Find the area of the region inside both \(C\) and \(T\) in terms of \(\theta\).
So the line from (iii) touches the curve. The area inside \(C\) and \(T\) is then simply a sector of the circle, and so its area is \(\dfrac{1}{2}r^2\theta = 2\theta\).
- Now let \(h = 6/7\). Show that the point \((8/5,6/5)\) lies on both the line (from part (iii)) and the circle \(C\).
Hence show that the area of the region inside both \(C\) and \(T\) equals
\[\dfrac{27}{35}+2\alpha,\]
where \(\alpha\) is an angle whose tangent, \(\tan \alpha\), you should determine.
You may use the fact that the area of a triangle with corners \((0,0), (a,b), (c,d)\) is \(\dfrac{1}{2}\vert ad-bc\vert\).
We have that \(\left(\dfrac{8}{5}\right)^2+\left(\dfrac{6}{5}\right)^2=2\), and \(\dfrac{6}{5} = -\left(\dfrac{6}{7}\right)\dfrac{8}{5}+3\left(\dfrac{6}{7}\right)\).
Thus when \(h = \dfrac{6}{7}, \left(\dfrac{8}{5},\dfrac{6}{5}\right)\) lies on both the line and the circle.
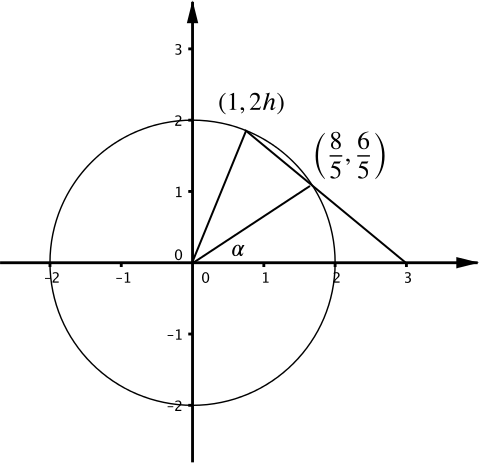
The sector with angle \(\alpha\) has area \(2\alpha\), where \(\tan \alpha = \dfrac{3}{4}\).
The triangular area inside \(C\) and \(T\) is (using the given formula) \(\dfrac{1}{2}\left\vert 1\times \dfrac{6}{5}-\dfrac{12}{7}\times\dfrac{8}{5}\right\vert = \dfrac{27}{35}\).
Thus the area inside \(C\) and \(T\) is \(\dfrac{27}{35}+2\arctan\left(\dfrac{3}{4}\right)\).

