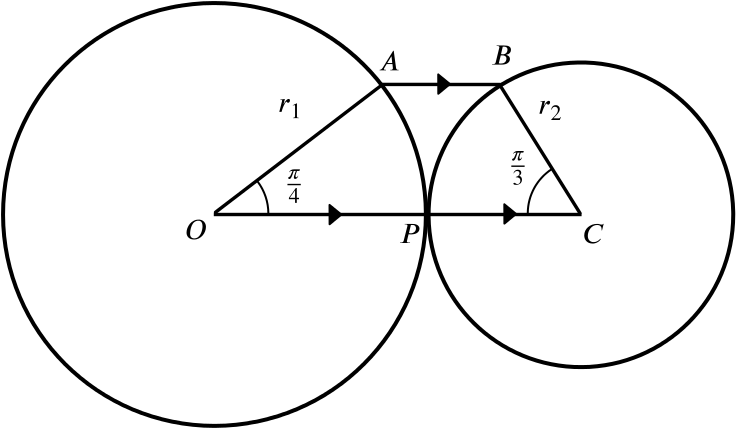
The figure shows two circles, centres \(O\) and \(C\), radii \(r_1\) and \(r_2\), which touch externally at \(P\). Given that \(A\hat{O}P=\dfrac{\pi}{4}\) radians, \(B\hat{C}P = \dfrac{\pi}{3}\) radians and \(AB\) is parallel to \(OPC\), show that \(\dfrac{r_1}{r_2} = \dfrac{\sqrt{6}}{2}\).
Could we create some right-angled triangles within the figure, and use trigonometric functions here?
Hence find the ratio of the areas of the sectors \(OAP\), \(CBP\).
What’s the formula for the area of a sector?

