The diagram below shows the parabola \(y=x^2\) and a circle with centre \((0,2)\) just ‘resting’ on the parabola. By ‘resting’ we mean that the circle and parabola are tangential to each other at the points \(A\) and \(B\).
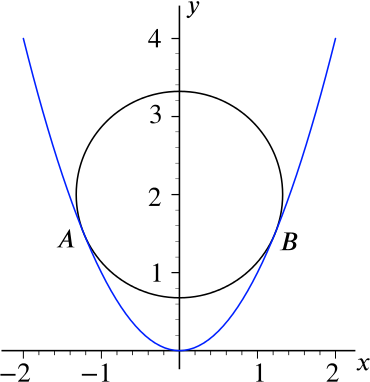
Let \((x,y)\) be a point on the parabola such that \(x \ne 0\). Show that the gradient of the line joining this point to the centre of the circle is given by \[\frac{x^2-2}{x}.\]
With the help of the result from the first part, or otherwise, show that the coordinates of \(B\) are given by \[\left(\sqrt{\frac{3}{2}},\frac{3}{2} \right).\]
Show that the area of the sector of the circle enclosed by the radius to \(A\), the minor arc \(AB\) and the radius to \(B\) is equal to \[\frac{7}{4} \cos^{-1} \left( \frac{1}{\sqrt{7}} \right) .\]
Suppose now that a circle with centre \((0,a)\) is resting on the parabola, where \(a > 0\). Find the range of values of \(a\) for which the circle and parabola touch at two distinct points.
Let \(r\) be the radius of a circle with centre \((0,a)\) that is resting on the parabola. Express \(a\) as a function of \(r\), distinguishing between the cases in which the circle is, and is not, in contact with the vertex of the parabola.

