The diagram below shows the parabola \(y=x^2\) and a circle with centre \((0,2)\) just ‘resting’ on the parabola. By ‘resting’ we mean that the circle and parabola are tangential to each other at the points \(A\) and \(B\).
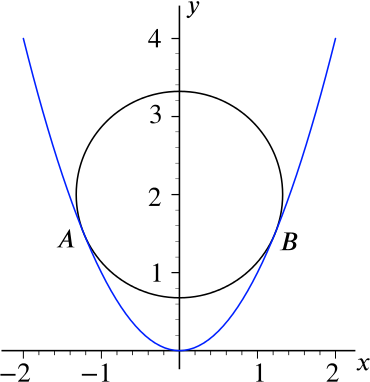
- Let \((x,y)\) be a point on the parabola such that \(x \ne 0\). Show that the gradient of the line joining this point to the centre of the circle is given by \[\frac{x^2-2}{x}.\]
The line segment joining the point \((x,x^2)\) and the centre of the circle \(C=(0,2)\) will have gradient \[\frac{x^2 - 2}{x - 0} = \frac{x^2 - 2}{x}.\] (Note that \(x \ne 0\), so we are not dividing by zero.)
- With the help of the result from the first part, or otherwise, show that the coordinates of \(B\) are given by \[\left(\sqrt{\frac{3}{2}},\frac{3}{2} \right).\]
For the circle to be tangent to the parabola at \(B\), the radius through \(B\) and the tangent to the parabola at \(B\) must be perpendicular.
Suppose \(B\) has coordinates \((b,b^2)\). Then the gradient of the parabola (and circle) at \(B\) is equal to \(2b\) (by differentiating the equation \(y=x^2\)).
We know the gradient of the radius through \(B\) from part (i), so we must have \[\frac{b^2 - 2}{b} =\frac{-1}{2b}\] (as perpendicular gradients multiply to \(-1\), which is the same as saying that one is the negative reciprocal of the other).
We can solve this by multiplying by \(2b\) to get \[2b^2 - 4 = -1,\] so \(b=\pm\sqrt{\dfrac{3}{2}}\). Since we must have \(b>0\) (from the diagram), we obtain \(b=\sqrt{\dfrac{3}{2}}\) and \(b^2 = \dfrac{3}{2}\), as required.
- Show that the area of the sector of the circle enclosed by the radius to \(A\), the minor arc \(AB\) and the radius to \(B\) is equal to \[\frac{7}{4} \cos^{-1} \left( \frac{1}{\sqrt{7}} \right) .\]
We draw on a right-angled triangle to help us here:
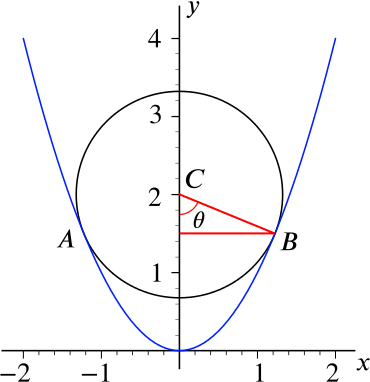
The square of the radius \(CB\) is \[r^2=\left(\sqrt{\frac{3}{2}}\right)^2+\left(\frac{3}{2}-2\right)^2= \frac{7}{4}\] and so the area of the circle is \(\pi r^2 = \dfrac{7}{4} \pi\).
The angle \(\theta\) is given by \[\cos\theta=\frac{2-\frac{3}{2}}{\sqrt{\frac{7}{4}}}=\frac{\frac{1}{2}}{\frac{1}{2}\sqrt{7}}=\frac{1}{\sqrt{7}}\] so \(\theta=\cos^{-1}(1/\sqrt{7})\).
The area of the sector is given by \(\dfrac{1}{2}r^2(2\theta)\), as the angle \(\angle ACB\) is \(2\theta\) by symmetry. Using our value of \(r^2\), we get \[\text{area}=\frac{1}{2}\times\frac{7}{4}\times2\cos^{-1}\left(\frac{1}{\sqrt{7}}\right)=\frac{7}{4}\cos^{-1}\left(\frac{1}{\sqrt{7}}\right)\] as required.
- Suppose now that a circle with centre \((0,a)\) is resting on the parabola, where \(a > 0\). Find the range of values of \(a\) for which the circle and parabola touch at two distinct points.
We now need to think about a new diagram:
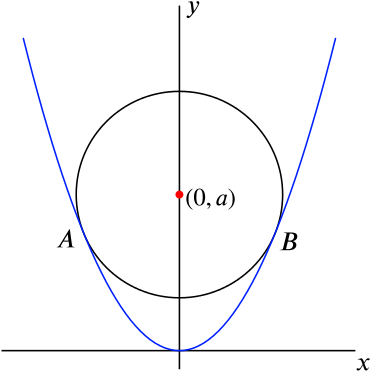
We consider an equation similar to that in part (ii), except with \(2\) replaced with a more general \(a\): \[\frac{b^2 - a}{b} =\frac{-1}{2b}.\] The solutions of this equation will be the intersections of the circle and parabola, and they will have the same gradient at these points, so the two will just touch.
We multiply by \(b\) and rearrange the equation to get \[b^2=a-\frac{1}{2},\] which has two distinct real solutions if and only if \(a>\dfrac{1}{2}\).
- Let \(r\) be the radius of a circle with centre \((0,a)\) that is resting on the parabola. Express \(a\) as a function of \(r\), distinguishing between the cases in which the circle is, and is not, in contact with the vertex of the parabola.
If \(0<a\le \dfrac{1}{2}\), then we know from part (iv) that the circle is resting on the vertex of the parabola, since it does not touch it in two places. In this case, it is clear that as the circle passes through \((0,0)\) and has its centre at \((0,a)\), its radius must be \(a\), so \(a=r\).
If \(a>\dfrac{1}{2}\), then there are two distinct points of contact, and we have \[r^2=b^2+(b^2-a)^2,\] where \(b\) is given by the formula in part (iv): \[b^2=a-\frac{1}{2}.\] Substituting this in, we find that \[\begin{align*} r^2&{}=\left(a-\frac{1}{2}\right)+\left(a-\frac{1}{2}-a\right)^2\\ &{}=a-\frac{1}{2}+\frac{1}{4}\\ &{}=a-\frac{1}{4} \end{align*}\]so that \[a=r^2+\frac{1}{4}.\]
As a check, when \(r=\dfrac{1}{2}\), which is the boundary between the two cases, the second formula gives \[a=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}=r,\] which is the same answer as given by the first formula.

