Find the equations of the two circles which each satisfy the following conditions:
the axis of \(x\) is a tangent to the circle,
the centre of the circle lies on the line \(2y = x\),
the point \((14,2)\) lies on the circle.
Let’s begin by sketching a diagram and see if this gives us any ideas on how to proceed. We sketch both circles and the second common tangent (required for the next part of the question). We know from (ii) that the centre of each circle has coordinates \((2a,a)\) for some \(a\). (Why must \(a\) be positive?) From (i) we know the corresponding radius is \(a\).
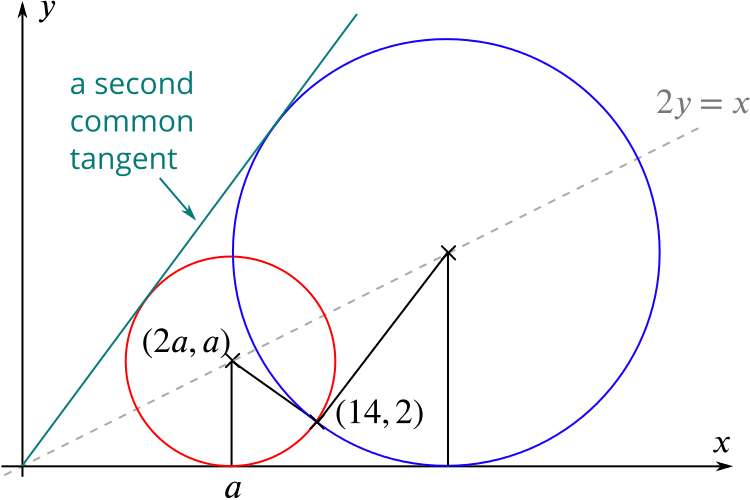
We focus on just one circle to begin with; when we solve the equations, the algebra should give us both circles as solutions, so we expect to find a quadratic equation arising.
We can see a lot of properties of this circle from looking at the diagram – in fact, we can write everything in terms of the one variable \(a\).
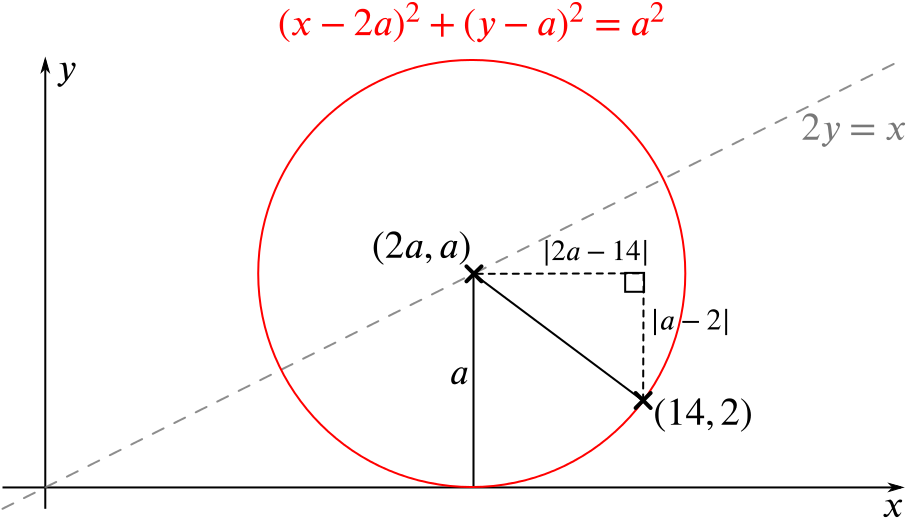
Since the distance from the centre to the \(x\)-axis and from the centre to the point \((14,2)\) must be the same (as they both lie on the circle), we need only solve \[a=\sqrt{(2a-14)^2+(a-2)^2}.\]
Squaring both sides, we obtain \[a^2=4a^2-56a+196+a^2-4a+4.\] Rearranging this, we find that \[4a^2-60a+200=0,\] or equivalently, \[a^2-15a+50=0.\]
We can factorise this as \[(a-5)(a-10)=0,\] and therefore \(a=5\) or \(a=10\), so the two circles are given by the formulae \[(x-10)^2+(y-5)^2=25\] and \[(x-20)^2+(y-10)^2=100.\]
Prove that the line \(3y = 4x\) is a common tangent to these circles.
For the second part of the question, we offer two different methods.
The first uses direct substitution to find where the line intersects the two circles.
The second uses the fact that the tangent to the circle will be perpendicular to the radius at that point.
Method 1
Expanding the equation of the first circle gives \[x^2 - 20x + y^2 - 10y + 100 = 0.\] Now substituting \(x = \frac{3}{4}y\) we have \[\begin{align} && \frac{9}{16}y^2 - 15y + y^2 - 10y + 100 &= 0\notag&&\quad\\ \Longrightarrow\quad&& \frac{25}{16}y^2 - 25y + 100 &= 0\notag\\ \Longrightarrow\quad&& y^2 - 16y + 64 &= 0 \label{eq:1}\\ \Longrightarrow\quad&& (y - 8)^2 &= 0.\notag \end{align}\]This has a single repeated root, and so the line is a tangent to the circle.
Alternatively, we could have begun by substituting \(y=\frac{4}{3}x\) and reached the same conclusion.
Also, instead of factorising on the last line, we could have observed that the discriminant of \(\eqref{eq:1}\) is \(16^2-4\times1\times64=0\), so that the quadratic has a repeated root.
An identical argument works for the second circle: \[\begin{align*} &&x^2 - 40x + y^2 - 20y + 400 &= 0&&\quad\\ \Longrightarrow\quad&& \frac{9}{16}y^2 - 30y + y^2 - 20y + 400 &= 0\\ \Longrightarrow\quad&& \frac{25}{16}y^2 - 50y + 400 &= 0\\ \Longrightarrow\quad&& y^2 - 32y + 256 &= 0\\ \Longrightarrow\quad&& (y - 16)^2 &= 0. \end{align*}\]So the line is also a tangent to this circle, and hence it is a common tangent to both of them.
Method 2
We aim here to find the point on \(3y=4x\) which is closest to the centre of the circle, by dropping a perpendicular to the line from the centre, and finding the intersection point. Now if this point lies on the circle, we know the line is a tangent.
The line \(3y = 4x\) has gradient \(\frac{4}{3}\). A line perpendicular to this will have gradient \(-\frac{3}{4}\). So the general equation of a perpendicular line will be \(y = -\frac{3}{4}x + c\).
Let’s say the centre of the first circle lies on this line, so substituting \((10,5)\) into the general equation gives \[\begin{align*} &5 = -\frac{3}{4} \times 10 + c\\ \Longrightarrow\quad& c = \frac{25}{2}. \end{align*}\]So the perpendicular line has equation \[y = -\frac{3}{4}x + \frac{25}{2}.\]
Then the point at which this line and the tangent intersect satisfies \[3y = 4x \text{ and } y = -\frac{3}{4}x + \frac{25}{2}\] Substituting in for \(y\) into the first equation gives \[\begin{align*} &&-\frac{9}{4}x + \frac{75}{2} &= 4x&&\quad\\ \Longrightarrow\quad&& -9x + 150 &= 16x\\ \Longrightarrow\quad&& 25x &= 150\\ \Longrightarrow\quad&& x &= 6 \end{align*}\]and on using \(3y=4x\), we find that \(y = 8\).
This is indeed a point on the circle: \((6 - 10)^2 + (8 - 5)^2 = 4^2 + 3^2 = 25\). Hence the line \(3y = 4x\) intersects the perpendicular line at a point on the circle, and so is a tangent line.
Using the same method for the second circle, we find that the intersection point is \((12,16)\) and so the line is also a tangent to this circle.

