In the diagram below is sketched the circle with centre \((1,1)\) and radius \(1\) and a line \(L\). The line \(L\) is tangential to the circle at \(Q\). Further, \(L\) meets the \(y\)-axis at \(R\), and the \(x\)-axis at \(P\) in such a way that the angle \(OPQ\) equals \(\theta\) where \(0<\theta<\dfrac{\pi}{2}\).
Show that the co-ordinates of \(Q\) are
\[(1+ \sin \theta, 1 + \cos \theta),\]
and that the gradient of \(PQR\) is \(- \tan \theta\).
We know the centre of the circle is at \((1,1)\).
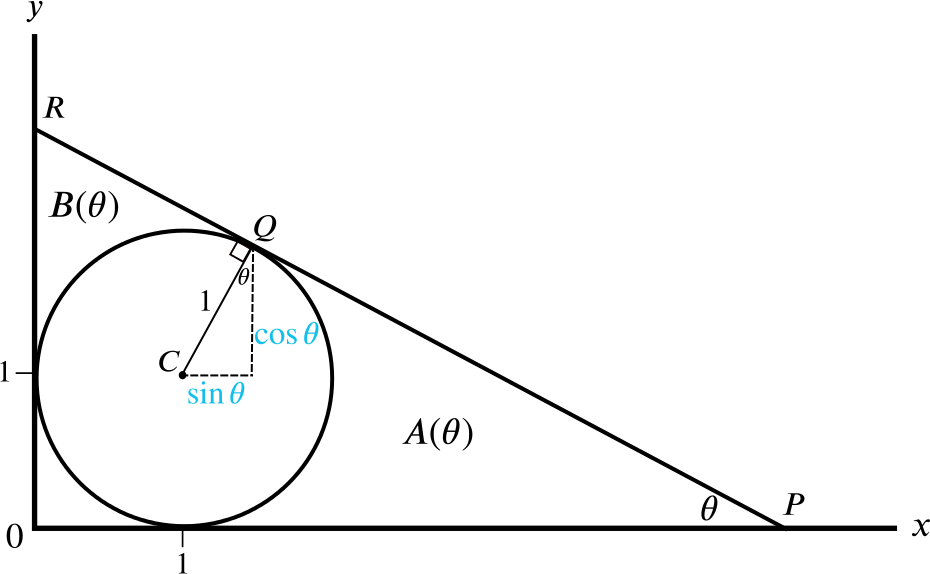
From the diagram, we can see that to get from the centre, \(C\), to the point \(Q\) we must travel “\(\sin\theta\)” horizontally and “\(\cos\theta\)” vertically, so
\[ Q= \quad (1 + \sin\theta, 1 + \cos\theta).\]
If we now let the length of \(PQR = \ell\), then \[\begin{align*} \text{gradient of } PQR &= \frac{\text{change in }y}{\text{change in }x} \\ &= \frac{-\ell\sin\theta}{\ell\cos\theta} \\ &= - \tan\theta, \qquad \text{as required.} \end{align*}\]Alternatively, we could find the gradient of the radius to \(Q\) and (because we know the radius and tangent are perpendicular) we can then find the gradient of the tangent \(PQR\).
The gradient of \(CQ\) is \(\dfrac{\cos\theta}{\sin\theta}\) (the change in \(y\) values \(\div\) the change in \(x\) values). The product of perpendicular gradients is \(-1\).
The tangent \(PQR\) is perpendicular to the radius, therefore: \[\begin{align*} \frac{\cos\theta}{\sin\theta} \times m &= -1, \\ \implies m &= -\frac{\sin\theta}{\cos\theta} \\ &= - \tan\theta, \qquad \text{as required.} \end{align*}\]Write down the equation of the line \(PQR\) and so find the co-ordinates of \(P\).
The line \(PQR\) has gradient \(-\tan\theta\) and goes through the point \((1 + \sin\theta, 1 + \cos\theta)\), and so has equation
\[y - (1 + \cos\theta) = -\tan\theta (x - (1 + \sin\theta)).\]
We’re not asked to give the equation of the line in any particular form, so we can leave it as is.
We could, if desired, simplify this answer:
\[\begin{align*} x &= 1 + \sin\theta + \frac{1}{\tan\theta} + \frac{\cos\theta}{\tan\theta} \\ &= 1 + \sin\theta + \cot\theta + \frac{\cos^2{\theta}}{\sin\theta} \\ &= 1 + \frac{\sin^2{\theta}}{\sin\theta} + \cot\theta + \frac{\cos^2{\theta}}{\sin\theta} \\ &= 1 + \frac{\left(\sin^2{\theta} + \cos^2{\theta} \right)}{\sin\theta} + \cot\theta \\ &= 1 + \frac{1}{\sin\theta} + \cot\theta \\ &= 1 + \cosec\theta + \cot\theta. \end{align*}\]If we’d looked at our diagram carefully, we could’ve arrived at the same answer:

Using \(\tan \theta = \dfrac{\text{opposite}}{\text{adjacent}}\), we see \(TP = \dfrac{1 + \cos\theta}{\tan\theta}\), and so
\[x = 1 + \sin\theta + \frac{1 + \cos\theta}{\tan\theta}.\]
Therefore the co-ordinates of \(P\) are \((1 + \cot \theta + \mathrm{cosec \hspace{1mm}} \theta, 0)\).
The region bounded by the circle, the \(x\)-axis and \(PQ\) has area \(A(\theta)\); the region bounded by the circle, the \(y\)-axis and \(QR\) has area \(B(\theta)\). (See diagram.)
Explain why
\[A(\theta) = B\left(\frac{\pi}{2} - \theta\right)\]
for any \(\theta\).
Let’s draw two diagrams - one with angle \(\theta\) at \(P\) and the other with angle \(\dfrac{\pi}{2} - \theta\) at \(P\):
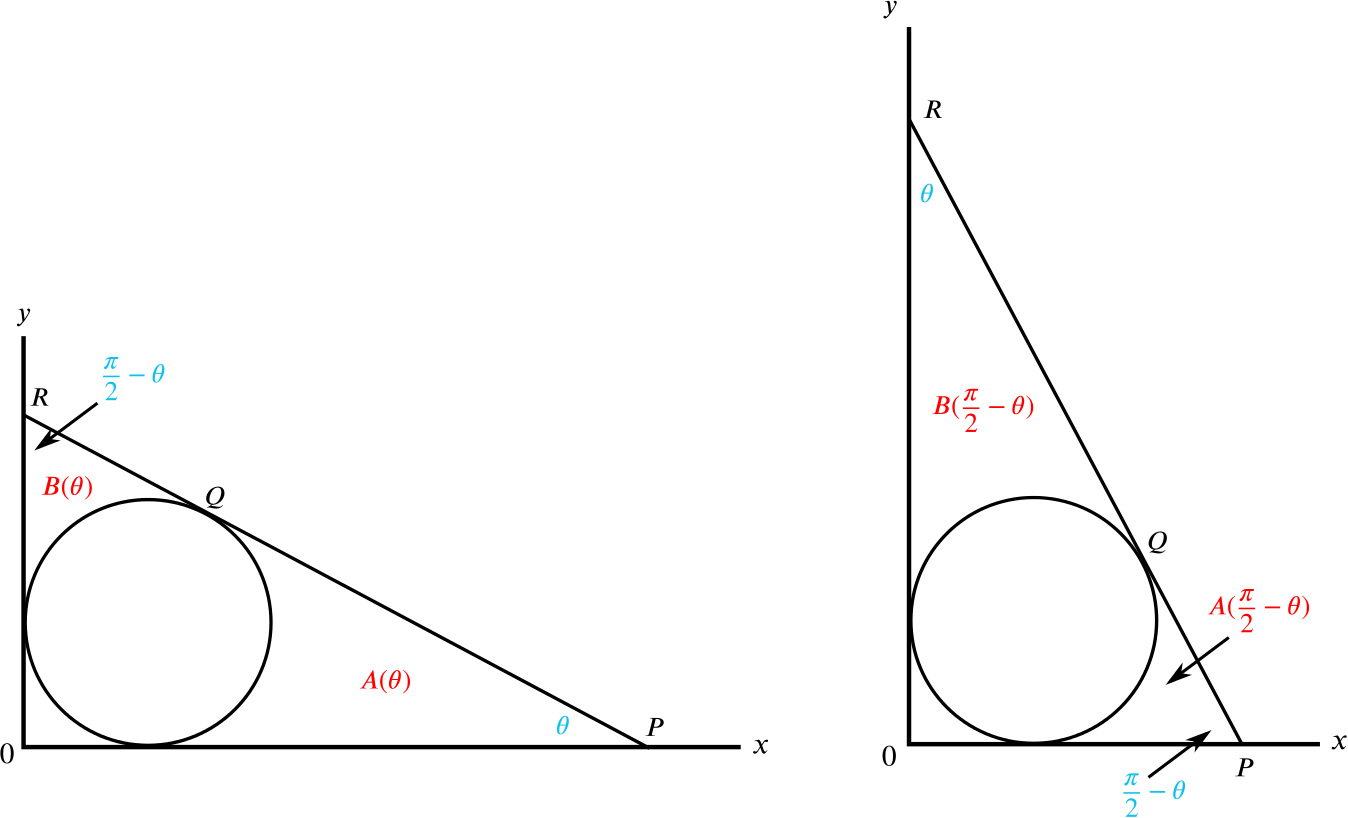
We can see simply from the symmetry of the diagrams that \(A(\theta) = B\left(\dfrac{\pi}{2} - \theta\right)\).
Calculate \(A\left(\dfrac{\pi}{4}\right)\).
To calculate \(A\left(\dfrac{\pi}{4}\right)\), let’s draw the diagram and see if it might help us.
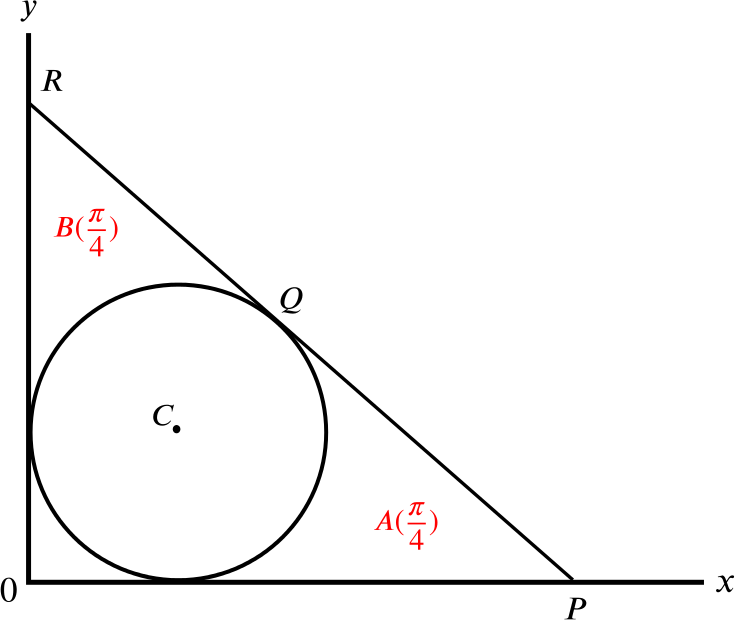
By symmetry, we see that \[A\left(\dfrac{\pi}{4}\right) = B\left(\dfrac{\pi}{4}\right).\]
Next, we need to know the lengths \(OP\) and \(OR\) of the triangle \(OPR\).
Using our final answer from (i), we have
\[\begin{align*} OP &= 1 + \frac{1}{\sin \dfrac{\pi}{4}} + \dfrac{\cos \dfrac{\pi}{4}}{\sin \dfrac{\pi}{4}} \\ &= 1 + \sqrt{2} + 1 \\ &= 2 + \sqrt{2}. \end{align*}\]Our triangle is isosceles, since both the angle at \(P\) and the angle at \(R\) are \(\dfrac{\pi}{4}\), so we have \(OR = OP\) and \[OR = 2 + \sqrt{2} \qquad \text{also.}\]
Now we can calculate the area of the whole triangle \(OPR\).
The shaded area in the diagram below is made up of a square of side length \(1\), and \(\dfrac{3}{4}\) of the circle (of radius \(1\)).
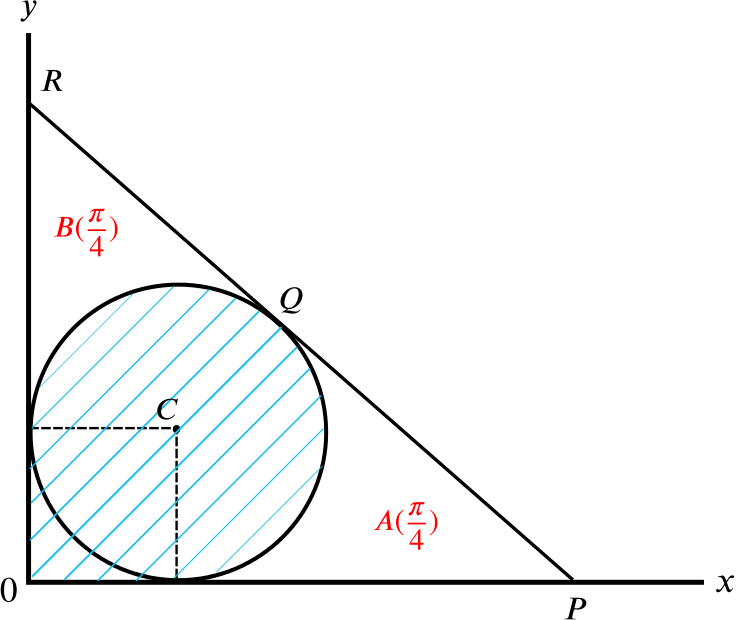
The shaded area is therefore: \[1 \times 1 + \frac{3}{4} \times \pi \times (1)^2 \qquad = \qquad 1 + \frac{3}{4} \pi.\]
The area of \(A\left(\dfrac{\pi}{4}\right)\) can now be found. We have
\[\begin{align*} A\left(\frac{\pi}{4}\right) &= \frac{1}{2} \left(\text{area of triangle }OPR - \text{shaded area} \right) \\ &= \frac{1}{2} \left(3 + 2\sqrt{2} - (1 + \frac{3\pi}{4}) \right) \\ &= \frac{1}{2} \left(2 + 2\sqrt{2} - \frac{3\pi}{4} \right) \\ &= 1 + \sqrt{2} - \frac{3\pi}{8}. \end{align*}\]Show that
\[A \left(\frac{\pi}{3} \right) = \sqrt{3} - \frac{\pi}{3}.\]

The length \(SP\) can be found from the triangle \(CSP\): we have
\[\begin{align*} \tan {\frac{\pi}{6}} &= \frac{CS}{SP} \\ \frac{1}{\sqrt{3}} &= \frac{1}{SP} \\ \text{so } \quad SP &= \sqrt{3}. \end{align*}\]Therefore the area of triangle \(CSP\) is \[\frac{1}{2} \times 1 \times \sqrt{3} \quad = \quad \frac{\sqrt{3}}{2}.\]
By symmetry, the area of triangle \(CQP\) is also \(\dfrac{\sqrt{3}}{2}\).
The area of the sector \(CQS\) is \[\frac{1}{3} \times \pi \times (1)^2 \quad = \quad \frac{1}{3} \pi.\]
Therefore we can now find the area \(A\left(\dfrac{\pi}{3}\right)\): we have
\[\begin{align*} A\left(\frac{\pi}{3}\right) &= \text{area of triangle } CSP + \text{area of triangle } CQP - \text{area of sector } CQS \\ &= \frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2} - \frac{\pi}{3} \\ &= \sqrt{3} - \frac{\pi}{3}, \qquad \text{as required.} \end{align*}\]
