What is the largest possible domain for each of the functions \(A\) to \(D\) and what is the corresponding range?
To find the domain and range for a function, it sometimes helps to sketch its graph.
We can sketch the graph of \(y=x^2\), and \(y=A(x)\) is a translation of it—in which direction?
\(A(x)\) can be evaluated for any input \(x\) so the domain of \(A(x)\) is all real numbers, which can be written as \(x\in\mathbb{R}\). The range is \(A(x)\geq-2\).
The domain and range are both the full set of real numbers, \(\mathbb{R}\).
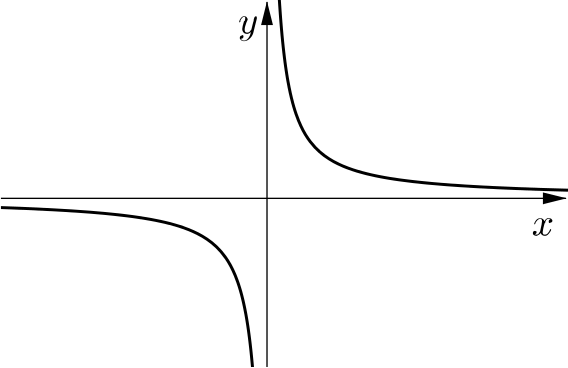
Allowing \(x=0\) would produce an undefined result so we need to restrict the domain to \(x\in\mathbb{R}, x\neq0\). No input value can achieve \(C(x)=0\) so the range is also restricted to the real numbers excluding \(0\).
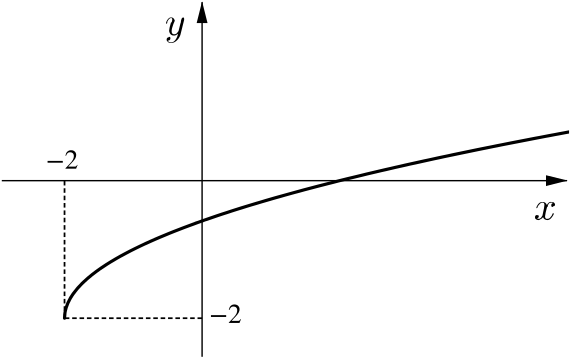The graph of this function is a translation of \(y=\sqrt{x}\).
The square root is undefined when \(x+2<0\) so the domain of this function is \(x\ge-2\).
We can evaluate \(D(-2)=-2\) and the square root function always increases as \(x\) increases, so the range is \(D(x)\ge-2\).
The functions above have been composed in some way to make the following new functions:
|
|
|
|
|
|
Can you work out which functions have been composed and in what order to make the new functions?
What are the domain and range for each composition of functions above?
Note that the composition might only be defined on a smaller domain than is possible for the function \(f(x)\).
We can see that this contains \(\dfrac{1}{x}\), suggesting function \(C\), and the form “\(something+4\)” hints at \(B\) being involved. \(B\left(\dfrac{1}{x}\right)=\dfrac{2}{x}+4\), giving us \[f(x)= \frac{2}{x}+4= BC(x).\]
The notation \(BC(x)\) is used to mean \(B\bigl(C(x)\bigr)\).
Using \(C(x)\) means the domain is \(x\neq0\) and since \(C(x)\neq0\) we cannot achieve 4 from \(BC(x)\). Hence the range is \(BC(x)\neq 4\). Can you illustrate this with a sketch of \(y=BC(x)\)?
We require a quadratic which leads us straight to \(A\). We don’t want any fractions, so we’re probably going to compose it with the linear function \(B\). Notice that we want the coefficient of \(x^2\) to be \(4\) which we could achieve by squaring \(B\).
We try \((2x+4)^2=4x^2+16x+16\) and see that \[f(x) = 4x^2+16x+14 = AB(x) .\]
We can allow any input value, hence the domain is \(\mathbb{R}\). As \(B(x)\in \mathbb{R}\), it follows that \(AB(x)\) has the same range as \(A(x)\), so \(AB(x)\geq-2\).
The fraction means we probably need to use \(C\), and the \(x^2\) indicates \(A\), but \(CA(x)=\dfrac{1}{x^2-2}\). We need the coefficient of \(x^2\) in the denominator to be \(2\), so first applying \(B\) before \(C\) will do this and helpfully it will also remove the unwanted \(-2\).
Since \(BA(x)=2(x^2-2)+4=2x^2\) we have \[f(x) =\frac{1}{2x^2} =CBA(x) .\]
To determine the domain and range we note that for \(A\) (which is applied first) the domain is the real numbers and the range is \(A(x)\geq-2\). This becomes the input of \(B\) so \(BA(x)\geq0\). The domain of \(C\) excludes \(x=0\) so we must exclude that output from \(B\). We do this by excluding the input of \(-2\). This means that the domain of \(CBA(x)\) is \(x\ne-2\) and it has range \(CBA(x)>0\).
Notice that the function \(\sqrt{x^2}\) gives the positive square root, so in order for \(DA(x)\) to equal \(x-2\) as required, \(x\) must be non-negative.
This gives \(DA(x)\) the restricted domain of \(x\ge0\). We need to check whether the domain is further restricted by the functions \(D\) and \(A\). The domain of \(A\) is \(\mathbb{R}\) which includes all of \(x\ge0\). Even with the restricted domain, the range is \(A(x) \ge-2\). This becomes the input of \(D\) and matches its domain, so \(DA\) has the same range as \(D\).
The composed function therefore has domain \(x\ge0\) and range \(DA(x) \ge-2\).
We might look at this and think about function \(C\), but we need the input to this to be \(4x+12\) which doesn’t immediately look like any of the other functions.
It might be a good idea to change tack and think what we can generate by composing some of the functions with themselves.
- Since \(A(x)\) is quadratic \(A^2(x)\) will be quartic. So this is not going to help!
The notation \(A^2(x)\) is used to mean \(A\bigl(A(x)\bigr)\).
\(B^2(x)=B(2x+4)=2(2x+4)+4=4x+12\)
That is what we need as input for \(C\) so \[f(x) =\frac{1}{4x+12} =CB^2(x) .\]
The domain and range of \(B\) are the real numbers, \(\mathbb{R}\), but the domain of \(C\) excludes zero so we must exclude \(4x+12=0\) from the input of the composition. Hence its domain is \(x\neq-3\) and its range is \(CB^2(x)\neq0\).
This is another case of a function composed with itself.
\[f(x) =x =\dfrac{1}{\left(\frac{1}{x}\right)} =C^2(x)\]
We might suppose that the domain and range of \(f(x)=x\) would be the real numbers, but because it was created by composing \(C(x)\) we have to exclude \(x=0\) from both.
Does this in fact mean that \(C^2(x)\) is not the same as the function \(f(x)=x\)?
