The function \[a(x)=x+1\] can be combined in a number of ways with each of the functions \[b(x)=2x-1, \quad b(x)=x^2-5x+8, \quad b(x)=x^2-5x-6\] to create a set of new functions. What functions are created by adding, subtracting and multiplying? Can you sketch them in the cells of the grid below?
You might prefer to choose from the graphs A to L which are provided as cards to print out.
| \(a(x)=\) \(x+1\) | \(a(x)+b(x)\) | \(a(x)-b(x)\) | \(a(x)\times b(x)\) |
|---|---|---|---|
| \(b(x)=\) \(2x-1\) |
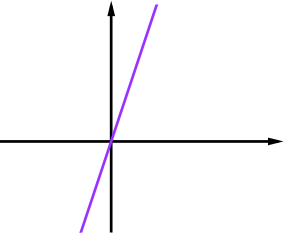
|
||
| \(b(x)=\) \(x^2-5x+8\) | |||
| \(b(x)=\) \(x^2-5x-6\) |

