The function \[a(x)=x+1\] can be combined in a number of ways with each of the functions \[b(x)=2x-1, \quad b(x)=x^2-5x+8, \quad b(x)=x^2-5x-6\] to create a set of new functions. What functions are created by adding, subtracting and multiplying? Can you sketch them in the cells of the grid below?
You might prefer to choose from the graphs A to L which are provided as cards to print out.
Top row, \(b(x)=2x-1\)
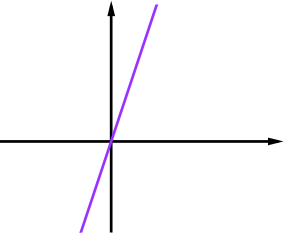
Here, \(a(x)\) and \(b(x)\) are both straight line functions. Adding and subtracting them will create other straight line functions and the correct ones can be found by checking their axis intercepts.
Multiplying two straight line functions will usually create a quadratic function.
In this case, the result is \(y=(x+1)(2x-1)\) which is an upward facing parabola with \(x\)-intercepts at \(-1\) and \(+\frac12\). So it must be graph K.
Can you find an example of straight line functions that do not create a quadratic when multiplied?
Middle row, \(b(x)=x^2-5x+8\)
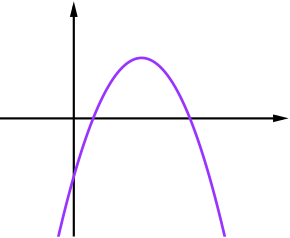
Adding, we get \(y = (x+1)+(x^2-5x+8) = x^2-4x+9\). This is an upward facing parabola, so it could be either I, J or K. It has a \(y\)-intercept of \(9\) so it must be graph I.
To check, we can see that it does not factorise, but we could write it in completed square form, \[y=(x-2)^2+5\] which shows that its vertex is at \((2,5)\) and it does not cross the \(x\)-axis.
Subtracting, we get \(y=-x^2+6x-7\). This is downward facing with \(y\)-intercept of \(-7\) so it could be graph F or G.
Completing the square, \(y = -(x-3)^2+2\), so its vertex is at \((3,2)\) and it therefore crosses the \(x\)-axis. It must be graph F.
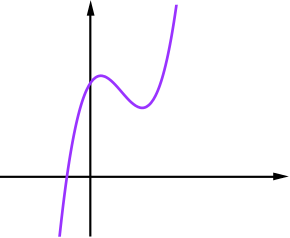
When we multiply a straight line function by a quadratic we expect to get a cubic function. Here, \(y=(x+1)(x^2-5x+8)\). We can see that this meets the \(x\)-axis at \(x=-1\) and that it has a \(y\)-intercept of \(8\). All three of graphs D, H and L meet the \(x\)-axis at some negative value of \(x\), but only H has a positive \(y\)-intercept. So this must be graph H.
Note that multiplying out the two brackets here would not be particularly helpful.
To check our choice of graph H, we could note that the graph has no other \(x\)-intercepts. What does this tell us about the quadratic factor, \((x^2-5x+8)\)?
Bottom row, \(b(x)=x^2-5x-6\)
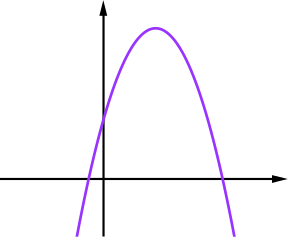
Adding, we get a quadratic that factorises. \[\begin{align*} y&=x^2-4x-5\\ &=(x-5)(x+1) \end{align*}\]It has \(x\)-intercepts at \(-1\) and \(5\) and \(y\)-intercept at \(-5\), so it must be graph J.
Subtracting, we get \[\begin{align*} y&=-x^2+6x+7\\ &=-(x-7)(x+1) \end{align*}\]This is downward facing with \(x\)-intercepts at \(-1\) and \(7\) and \(y\)-intercept at \(7\), so it must be graph E.
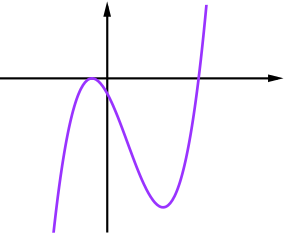
Multiplying, we get another cubic. This time we can factorise it further. \[\begin{align*} y&=(x+1)(x^2-5x-6)\\ &=(x+1)(x-6)(x+1) \end{align*}\]It has a repeated root at \(x=-1\) and another root at \(x=6\) so it must be graph D.