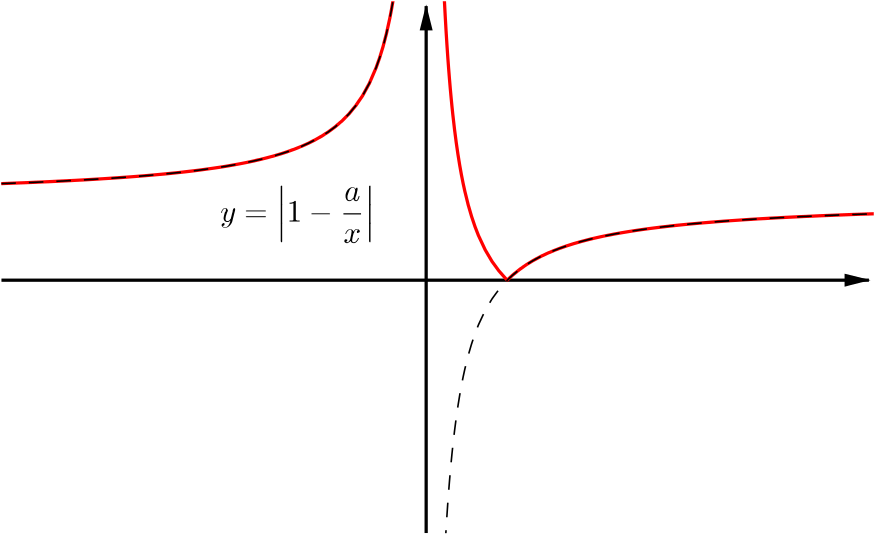
Hence sketch the curves \[\text{(iii)}\ y = \left|\frac{x-a}{x}\right|,\qquad \dots\]
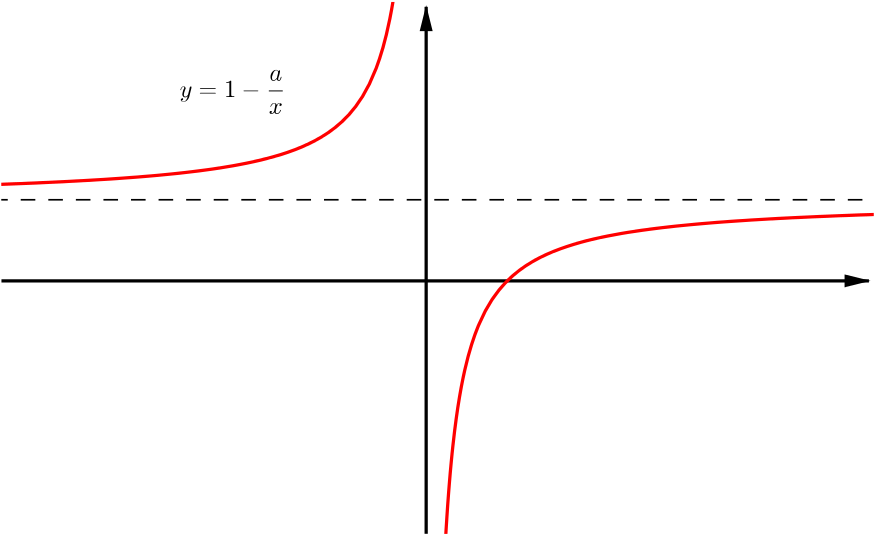
As we already have a sketch of the graph \(y=\frac{x-a}{x}\), we need only consider the effect that taking the absolute value has on the graph.
Every point on the curve with a positive \(y\) co-ordinate is fixed and every point with a negative \(y\) co-ordinate is reflected in the \(x\)-axis. This gives us the following sketch.
Hence sketch the curves \[\dots,\qquad \text{(iv)}\ y^2 = \frac{x^2-a^2}{x^2}.\]
Approach 1
We start by rewriting our equation as
\[\begin{equation} y=\pm \sqrt{1-\frac{a^2}{x^2}}. \label{equation} \end{equation}\]Firstly, we note that if \(-a<x<a\), then \(1-\frac{a^2}{x^2} <0\) and so \(\eqref{equation}\) has no solutions. This means that our curve only has points with \(x\ge a\) or \(x \le -a\). We will consider the sketch of \(y=1-\frac{a^2}{x^2}\), from (ii), in this range and aim to plot the square roots. This is, for each point \((x,y)\) on this curve, we want to include the points \((x,\pm \sqrt{y})\) in our sketch of \(\eqref{equation}\).

If \(y<1\), then the vertical distance decreases and, if \(y>1\), the vertical distance increases. Therefore, we get the following graph for the positive root \(y=+\sqrt{1-\frac{a^2}{x^2}}\).

To plot the other root \(y=-\sqrt{1-\frac{a^2}{x^2}}\), we can simply add the reflection in the \(x\)-axis.
We now need only consider the points \((\pm a,0)\) and the angles that the curves make at these points. Comparing to the graph of \(y=\sqrt{x}\), we would not expect the curve to be sharp at these points. Hence, we will include the information that the curve intersects the \(x\)-axis at right-angles in our final sketch.
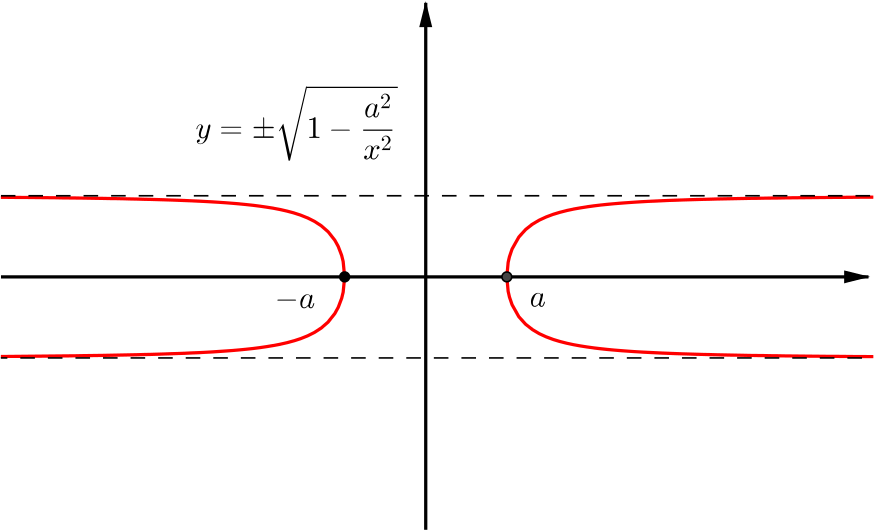
Similarly to before, the equations of the asymptotes are \(y=\pm 1\) and the points of intersection are at \(x=\pm a\).
The full details as to why this argument works will be touched on at university-level, but there are a number of ways that we can convince ourselves of this result none-the-less. For example, would we expect these points to be sharp if we rewrote the curve in the form \(x=\pm\frac{a}{\sqrt{1-y^2}}\)? Alternatively, what would we expect if we used calculus to calculate the gradient of the curve at these points? What does this tell us?
Approach 2
We begin by rewriting our equation as
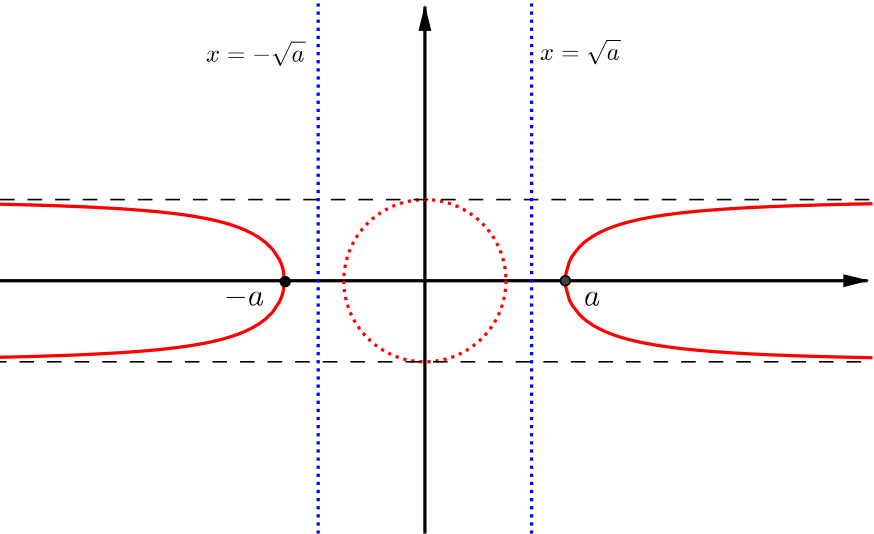
\[\begin{equation} y^2 + \left(\frac{a}{x}\right)^2 = 1. \label{eq:4} \end{equation}\]As this looks similar to the equation for a circle, we will begin by considering the graph of the unit circle \(y^2+x^2=1\).
To get the graph of equation \(\eqref{eq:4}\), we want to swap the \(x\) for \(\frac{a}{x}\). This is equivalent to finding another point \(x'\) such that \(xx'=a\) (i.e. point \(x'\) for which the geometric mean of \(x\) and \(x'\) are on the lines \(x=\pm\sqrt{a}\)). This is equivalent to inversion in the lines \(x=\pm\sqrt{a}\) and so each half of the circle can be projected outwards in the \(x\)-direction, as shown.