Let \[f(x)=x+1\qquad\text{and}\qquad g(x)=2x.\] We will, for example, write \(fg\) to denote the function “perform \(g\) then perform \(f\)” so that \[fg(x)=f(g(x))=2x+1.\] If \(i\geq 0\) is an integer we will, for example, write \(f^i\) to denote the function which performs \(f\) \(i\) times, so that \[f^i(x)=\underbrace{fff......f}_\text{$i\,\text{times}$}(x)=x+i.\]
- Show that \[f^2g(x)=gf(x).\]
\[f^2g(x)=f(f(g(x)))=((2x)+1)+1=2x+2=2(x+1)=g(f(x))=gf(x).\]
- Note that \[gf^2g(x)=4x+4.\] Find all the other ways of combining \(f\) and \(g\) that result in the function \(4x+4\).
When a question asks for all ways of doing something, or all solutions, we need to find a way to show we haven’t missed any. Also, question parts are often closely related and the earlier parts can be very useful for answering the later parts.
Since we need to make \(4x+4\), we must need two \(g\)s and between one and four \(f\)s in some order. Using the equation from part one, we have \[gf^2g(x)=g(f^2g)(x)=g(gf)(x)=g^2f(x)\] and \[gf^2g(x)=(gf)fg(x)=(f^2g)fg(x)\] which gives \[f^2gfg(x)=f^2(gf)g(x)=f^2(f^2g)g(x)=f^4g^2(x)\] and any more rearrangements would just take us back to one of these options.
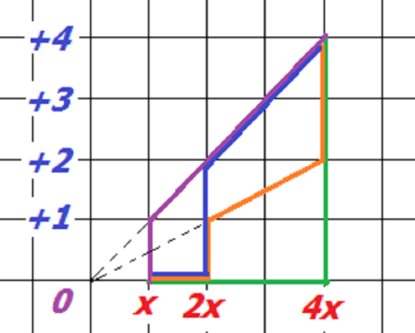
Therefore the four possible ways are: \[gf^2g(x),\quad g^2f(x),\quad f^2gfg(x),\quad f^4g^2(x)\] and nothing else.
The four ways are shown in this diagram in green, blue, orange and purple.
- Let \(i,j,k\geq0\) be integers. Determine the function \[f^igf^jgf^k(x).\]
From the example in the question, \(f^i(x)=x+i\), so, \[f^igf^jgf^k(x)=2(2(x+k)+j)+i=4x+i+2j+4k\]
- Let \(m\geq0\) be an integer. How many different ways of combining the functions \(f\) and \(g\) are there that result in the function \(4x+4m\)?
For any m, there will still only be two \(g\)s.
Thus any function will be of the form \(f^igf^jgf^k(x)\) with integers \(i,j,k\geq 0\) as in part (iii) with \[i+2j+4k=4m\]
Approach 1
Since \(i,j\geq0\), the value of k is constrained by \(0\leq k\leq m\).
Then, given k, the value of j is constrained by \(0\leq j\leq 2m-2k\), since \(i\geq 0\) and \(i+2j=4m-4k\).
Once \(j\) and \(k\) are determined, \[i=4m-4k-2j,\] so \(i\) is also uniquely determined. Therefore the number of possible solutions is: \[\begin{align*} \sum_{k=0}^m \bigg(\sum_{j=0}^{2m-2k}&1\bigg)\\ &=\sum_{k=0}^m2m-2k+1\\ &=\sum_{k=0}^m(2m+1)-2\sum_{k=0}^mk\\ &=(m+1)(2m+1)-2\times \frac{1}{2} m(m+1)\\ &=(m+1)^2. \end{align*}\]Approach 2
So how many ways are there of picking \(i, j\) and \(k\) so that \(i+2j+4k=4m\)? We can draw up a table.
| \(k\) | \(m\) | \(m-1\) | \(m-1\) | \(m-1\) | \(m-2\) | \(m-2\) | \(m-2\) | \(m-2\) | \(m-2\) | \(m-3\) | \(\ldots\) | \(0\) |
| \(j\) | \(0\) | \(2\) | \(1\) | \(0\) | \(4\) | \(3\) | \(2\) | \(1\) | \(0\) | \(6\) | \(\ldots\) | \(0\) |
| \(i\) | \(0\) | \(0\) | \(2\) | \(4\) | \(0\) | \(2\) | \(4\) | \(6\) | \(8\) | \(0\) | \(\ldots\) | \(4m\) |
So adding up the possibilities, we have \(1 + 3 + 5 + ... + (2m+1) = (m+1)^2\), since this is an arithmetic series with \(a = 1, d = 2, n = m+1\).

