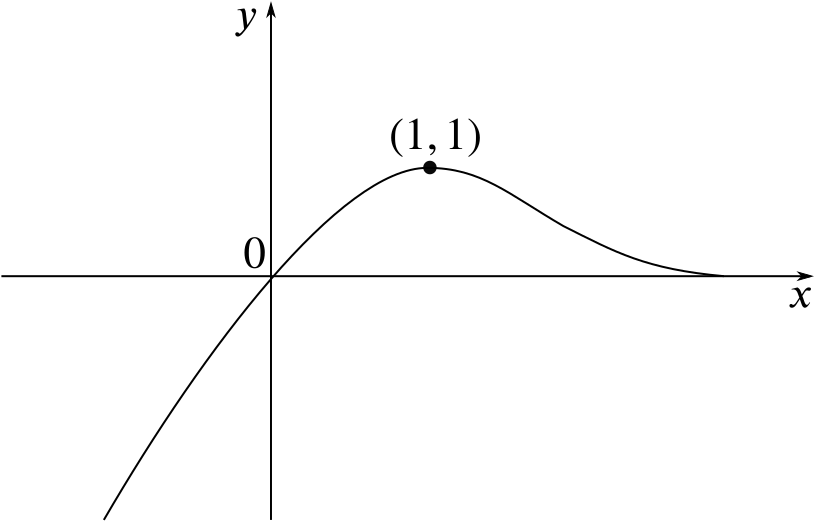
The diagram shows the graph for \(y = f(x)\). The curve passes through the origin, and has a maximum point at \((1, 1)\). Sketch, on separate diagrams, the graphs of
- \(y = f(x) + 2\),
… giving the coordinates of the maximum point in each case.
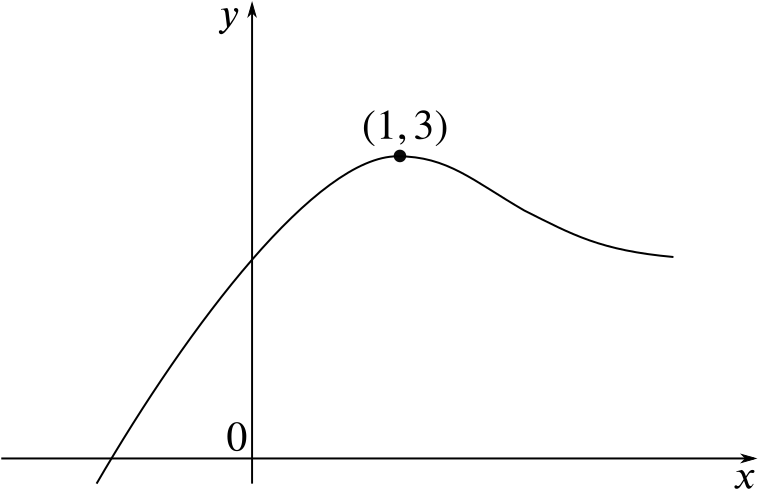
The graph of the function \(y = f(x) + 2\) can be obtained from the graph of the original function \(f\) by raising the \(y\)-coordinate of each point on the graph by \(2\). In particular, the maximum becomes \((1, 3)\). The new graph looks like this.
- \(y = f(x + 2)\),
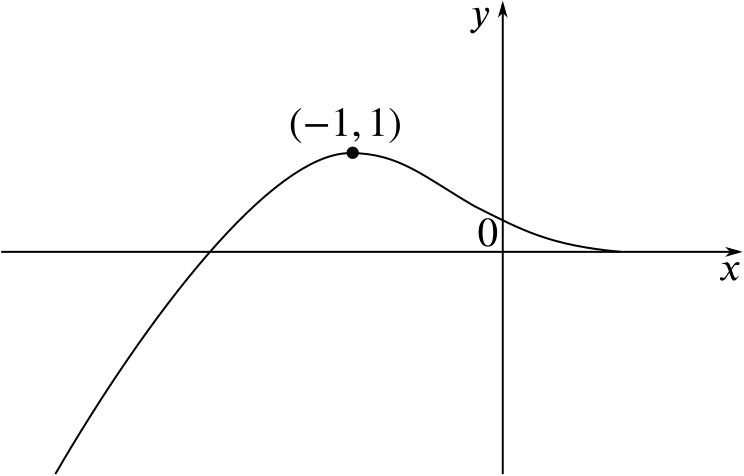
You might expect a shift to the right, but if you think that the \(y\)-coordinate associated with \(x = 0\) on the old graph is now associated with \(x = -2\) on the new graph, you can see it is a translation to the left.
In particular, the maximum becomes \((-1, 1)\). The new graph looks like this.
- \(y = f(2x)\).
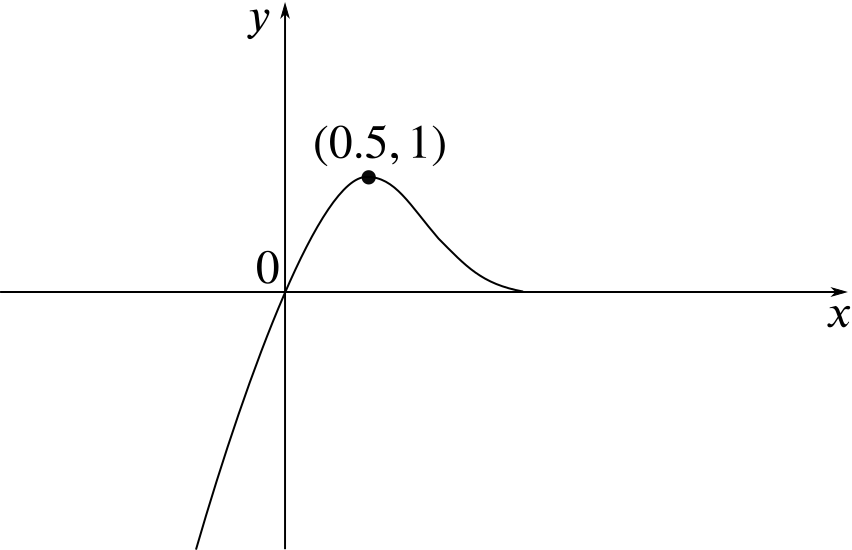
The graph of the function \(y = f(2x)\) can be obtained from the graph of the original function \(f\) by compressing the graph by a scale factor of \(2\) in the \(x\)-direction.
We could describe this as a stretch in the \(x\)-direction with scale factor \(\dfrac{1}{2}\).
In particular, the maximum becomes \((0.5, 1)\). The new graph looks like this.
Can you think of an \(f(x)\) that would give something like the starting graph above? You might use graphing software to try a few functions.

