Give definitions of each of the functions \(fg\) and \(f^{-1}\), and state, in each of the following cases, a relationship between the graphs of
\(f\) and \(fg\),
\(f\) and \(f^{-1}\).
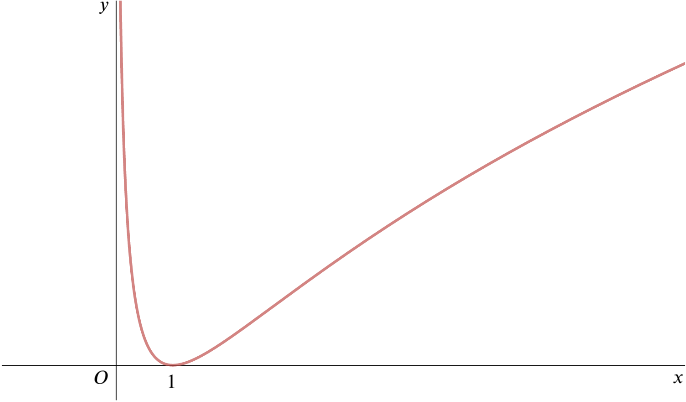
The diagram shows a sketch of the graph \(y=hf(x)\). State how the sketch shows that \(hf\) is not one–one, and prove that, if \(\alpha\) and \(\beta\), where \(0<\alpha <\beta\), are such that \(hf(\alpha)=hf(\beta)\), then \(\alpha=g(\beta)\).
- The function \(\phi\) is defined by \[ \phi : x \mapsto hf(x),\qquad (0 < x \leq 1).\] Sketch the graph of \(\phi^{-1}\), and give an explicit expression in terms of \(x\) for \(\phi^{-1}(x)\).

