- Give definitions of each of the functions \(fg\) and \(f^{-1}\)
For \(fg\): composing \(f\) and \(g\) we find \[fg(x) = f[g(x)]=\ln\left(\frac{1}{x}\right)=-\ln x.\]
For \(f^{-1}\): rearranging the formula \(y=\ln x\) to make \(x\) the subject we find \(x=e^y\), so \[f^{-1}(x)=e^x.\]
…(a) state a relationship between the graphs of \(f\) and \(fg\)
Reflection in the \(x\)–axis.
…(b) state a relationship between the graphs of \(f\) and \(f^{-1}.\)
Reflection in the line \(y=x\).
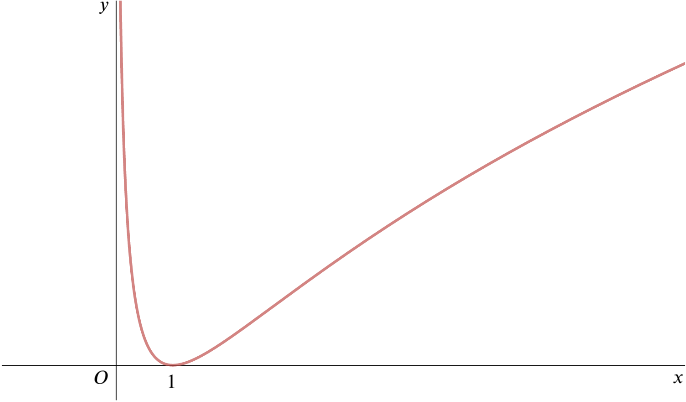
The diagram shows a sketch of the graph \(y=hf(x)\). State how the sketch shows that \(hf\) is not one–one.
There are horizontal lines that cut the graph twice. In fact, for every positive \(y\)-value, there are two \(x\)-values that \(hf\) maps to the \(y\)-value.
… and prove that, if \(\alpha\) and \(\beta\), where \(0<\alpha <\beta\), are such that \(hf(\alpha)=hf(\beta)\), then \(\alpha=g(\beta)\).
The composition \(hf(x)=h(\ln x)=(\ln x)^2\).
\[\begin{align*} hf(\alpha) &= hf(\beta) \\ \Longrightarrow(\ln \alpha)^2 &= (\ln\beta)^2\\ \Longrightarrow \ln \alpha &= -\ln\beta. \end{align*}\] We must have the minus sign here, since \(\alpha \neq \beta\). Now we have \[\begin{align*} \ln \alpha &= -\ln\beta = \ln\left(\frac{1}{\beta}\right)\\ \Longrightarrow \alpha &= \frac{1}{\beta}=g(\beta). \end{align*}\]From the graph we see that if \(\alpha < \beta\), \(0<\alpha < 1\) and \(\beta > 1\).
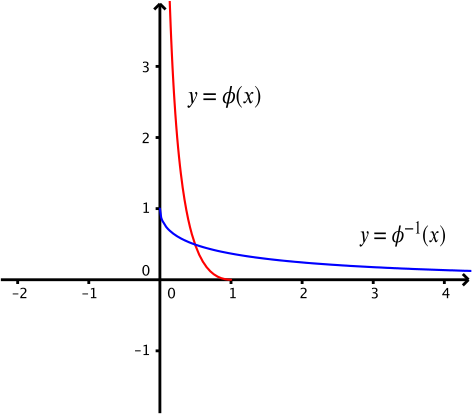
- The function \(\phi\) is defined by \[ \phi : x \mapsto hf(x),\qquad (0 < x \leq 1).\] Sketch the graph of \(\phi^{-1}\), and give an explicit expression in terms of \(x\) for \(\phi^{-1}(x)\).
Switching \(x\) and \(y\) we find that the inverse of \(\phi\) is \[\phi^{-1}(x)=e^{-\sqrt{x}}.\] We can find the graph of the inverse of a one-one function by reflecting in the line \(y=x\).
Below are the graphs of both \(y=\phi(x)\) and \(y=\phi^{-1}(x)\).