The severity of an earthquake is measured and recorded as its local magnitude, \(M_L\), often referred to as its position on the Richter Scale. For instance the New Zealand earthquake of 2011 was of magnitude \(6.1\) (according to USGS).
The magnitude is defined as a function of \(A\), the maximum amplitude of horizontal displacement of the earth’s surface at a distance of \(\quantity{100}{km}\) from the epicentre, \[M_L=\log_{10}\left(\frac{A}{A_0}\right)\]
where \(A_0\) is a constant displacement chosen as a reference value by Charles Richter in 1935. \[A_0=\quantity{1}{\mu m}=\quantity{10^{-6}}{m}\]
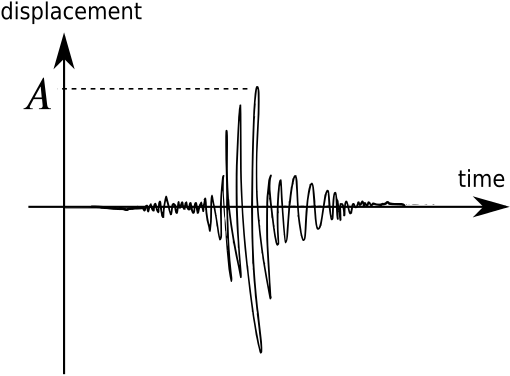
What is the magnitude of an earthquake causing a displacement, \(A\), equal to
- \(\quantity{1.0}{\mu m}\)?
- \(\quantity{1.0}{cm}\)?
- \(\quantity{30}{cm}\)?
What was the surface displacement for the following earthquakes? What might that have looked or felt like?
- New Zealand, 2011, \(M_L=6.1\)
- Lincolnshire, 2008, \(M_L=5.2\)
- Chile, 1960, \(M_L=9.5\)
What makes a logarithmic scale useful for describing phenomena like this? Do you know of any other commonly used logarithmic scales?

