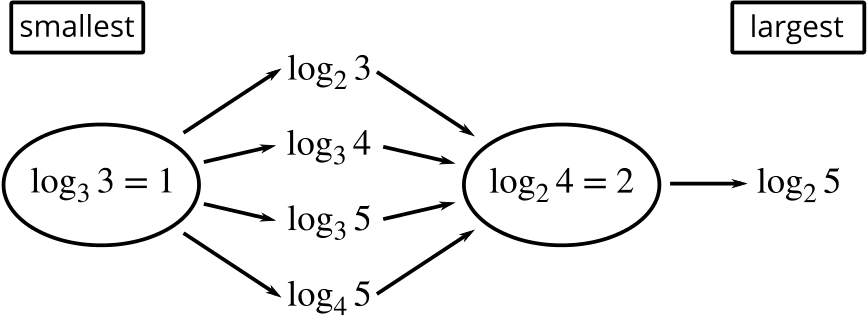
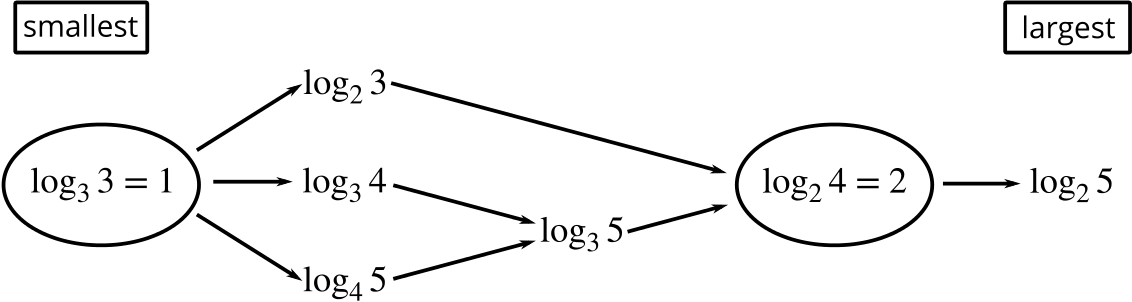
Can you, without using a calculator, arrange these logarithms into order of increasing value?
\[\log_{4} 5 \quad \log_{2} 5 \quad \log_{3} 4 \quad \log_{3} 3 \quad \log_{3} 5 \quad \log_{2} 4 \quad \log_{2} 3\]
Initial observations
- We can write down exact values for two of these logarithms.
- Since \(\log_3 5\) is the power of \(3\) that would give us \(5\) and \(3^1<5<3^2\) we know the value of \(\log_3 5\) must lie between \(1\) and \(2\). Can you do the same for other logarithms in the list and use the results to put some of them in order?
Increasing or decreasing?
If we take a series of logarithms all with the same base, we might assume that \(\log\) of a bigger number will have a bigger value. In other words, the function \(\log x\) is increasing.
Is this always true, or only for some values of \(x\)? Does it depend on the base of the logarithm?
If it is true for the logarithms in our list, we can use this fact to put some of them in order.
Changing bases
If instead, we take a series of logarithms of the same number but to different bases, would these increase or decrease? Think about \(\log_2 8\) and \(\log_4 8\). Can we use this idea to order some of our logarithms?
More generally, we are asking whether the function \(\log_x a\) is increasing or decreasing - does it depend on the value of \(a\)? You could try using graphing software such as Desmos (find \(\log_a\) on its functions menu).
Another way to compare these logarithms of the same number would be to use the rule for changing the base: \[\log_a b=\log_a c \times \log_c b\text{ .}\]
For instance, to compare \(\log_3 5\) and \(\log_4 5\), we could write \(\log_3 5 = \log_3 4\times\log_4 5\) and then note that \(\log_3 4 > 1\), and so \(\log_3 5 > \log_4 5\).
Estimating values
It is possible to find some other upper and lower bounds within our list of logarithms by using approximations for the square roots of \(2\) and \(3\):
We know that \(2^\frac{1}{2}\approx1.4\), so \(2^\frac{3}{2}=2\times2^\frac{1}{2}\approx2.8\).
Therefore \(\frac{3}{2}\approx\log_2{2.8}\), and hence \(\log_2{3}>\frac{3}{2}\).
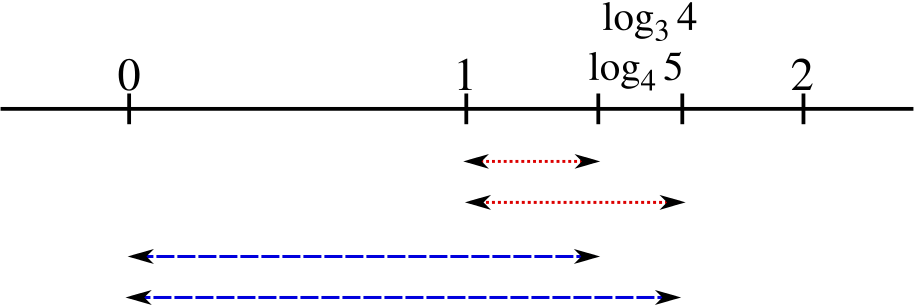
Can you use an approximate value of \(\sqrt 3\) to find an upper bound for \(\log_3 5\)?
Increasing or decreasing again
We shall now look at two possible ways of comparing \(\log_3 4\) and \(\log_4 5\) which is the last unknown pairing in our lineup.
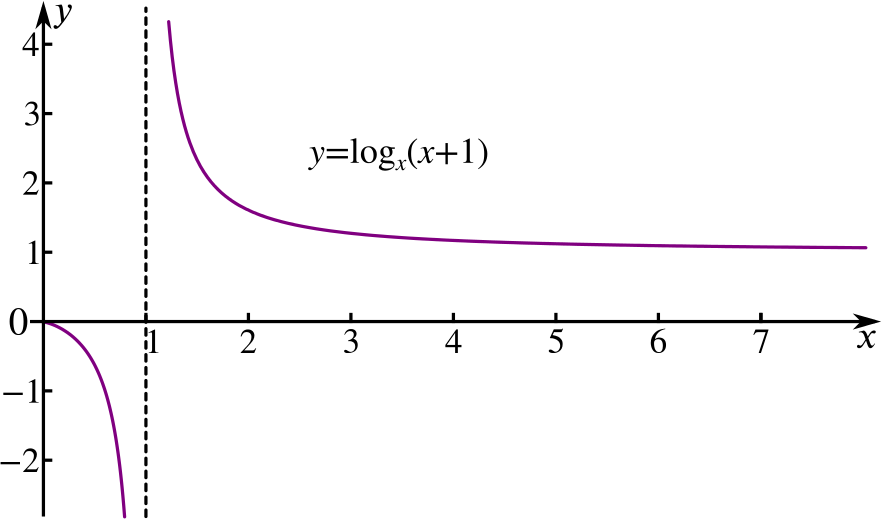
Firstly, notice that in each of these remaining logarithms, the base is one less than the number whose logarithm we are taking. We could think of them as values of the function \(\log_x{(x+1)}\). Is this an increasing or decreasing function? Think about its value when \(x=2\) and when \(x\) is very large. You could use Desmos to explore it.
Different differences
Another way to compare \(\log_4 5\) and \(\log_3 4\) would be to work out the difference between them, \[d=\log_3 4 - \log_4 5 \text{ .}\] If we can show that the difference is positive then we can put the two logarithms in order.
This looked promising but it has only told us that \(d\) is greater than some negative number, so it is not helpful in this case.
Can you use the subtraction law of logarithms to rearrange this and show that \(d>0\)?
We have shown alternative methods for some steps of the argument. What are the advantages and disadvantages of the different methods?
Can you add some more logarithms to the list and use similar techniques to insert them in the lineup?