Which of the following have no real solutions?
(i) \(2x<2^x<x^2\quad\) (ii) \(x^2<2x<2^x\quad\) (iii) \(2^x<x^2<2x\quad\)
(iv) \(x^2<2^x<2x\quad\) (v) \(2^x<2x<x^2\quad\) (vi) \(2x<x^2<2^x\)
A (i) and (iii),\(\quad\) B (i) and (iv),\(\quad\) C (ii) and (iv),\(\quad\) D (ii) and (v),\(\quad\) E (iii) and (v)
It helps here to think of the graphs \(y = 2x\), \(y = 2^x\) and \(y = x^2\).
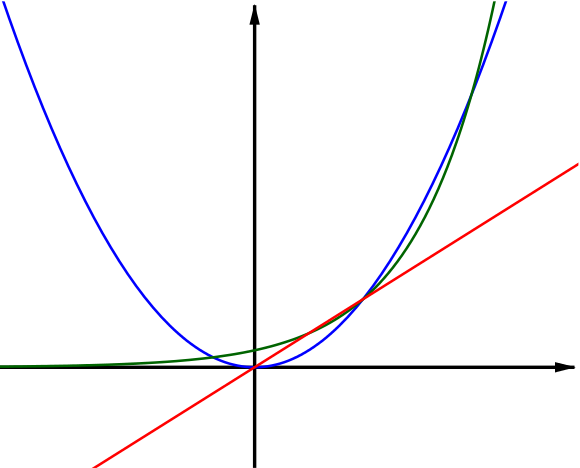
The curves \(y = 2x\) and \(y = x^2\) meet at the origin.
When \(x = 1\), \(2^x = 2x\).
When \(x = 2\), \(2^x = x^2=2x\).
When \(x = 4\), \(2^x = x^2\).
From these facts, we can sketch the three curves and note what order they must be in between their intersections.
The red curve is \(y = 2x\), the blue curve is \(y=x^2\) and the green curve is \(y=2^x\).
We can see that the possible orders are
red < green < blue, red < blue < green, blue < red < green, blue < green < red.
So the green curve cannot be the bottom one, and that rules out (iii) and (v). The answer is E.

