How many real roots does $8^x+4=4^x+2^{x+2}$ have?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Ref: R7606

Printable/supporting materials Printable version Fullscreen mode Teacher notes

Solution

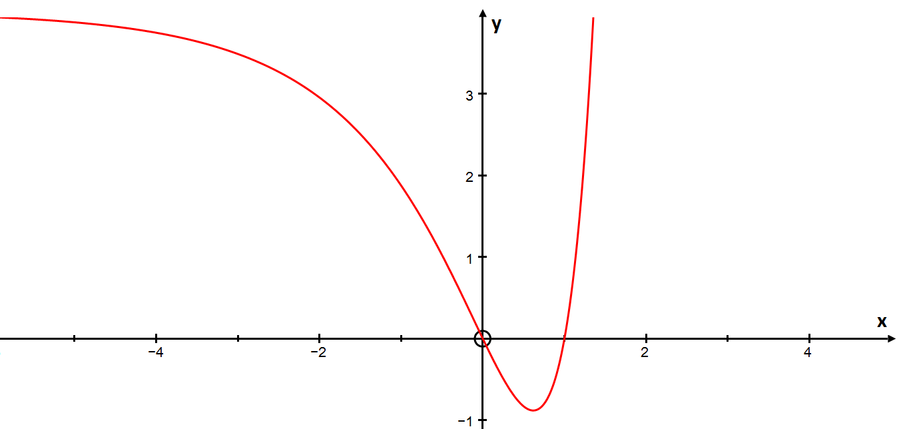
The equation \[8^x+4=4^x+2^{x+2}\] has

no real solutions;
one real solution;
two real solutions;
three real solutions.

[A real solution is one that lies on the number line.]

First set $y=2^x$. Then the equation can be rewritten as \[\begin{align*} &y^3+4=y^2+4y\\ \iff &y^3-y^2-4y+4=0. \end{align*}\] The left hand side can be factorised (by noticing that if we substitute $y=1$ then we have a solution). \[\begin{align*} &(y-1)(y^2-4)=0\\ \iff &(y-1)(y-2)(y+2)=0 \end{align*}\]

So the possible solutions are $y=1$, $y=2$, $y=-2$. But $y=2^x>0$ for real $x$, so valid solutions occur when $y=1$ or $y=2$.

This gives the solutions $x=0$ and $x=1$ respectively, but since we’re only asked how many solutions there are, we don’t actually need to find them (provided we can be sure they exist!)

So the equation has two real solutions. The answer is (c).

The curve whose roots are those required. — The curve $y=8^x+4-4^x-2^{x+2}$

Previous Next

Exponentials & Logarithms

How many real roots does $8^x+4=4^x+2^{x+2}$ have? Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Solution

Station

Lines

How many real roots does $8^x+4=4^x+2^{x+2}$ have?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource