Draw the graph of \(y=3^x\) for values of \(x\) from \(-2\) to \(+2\), plotting at least nine points. [Take \(\quantity{2}{cm}\) as unit on the axis of \(x\), and \(\quantity{1}{cm}\) as unit on the axis of \(y\).]
We first draw our axes as instructed. Use graph paper or squared paper and make sure that \(1\) on the \(x\)-axis is twice the length of \(1\) on the \(y\)-axis as in the picture:

The question asks us to plot at least nine points. We will plot \(-2\), \(-3/2\), \(-1\), …, \(3/2\), \(2\). We first compute the values of \(y\) at these points.
| \(x\) | \(y\) | Approximate value |
|---|---|---|
| \(-2\) | \(\frac{1}{9}\) | \(0.111\) |
| \(-\frac{3}{2}\) | \(\frac{1}{\sqrt{3^3}}\) | \(0.192\) |
| \(-1\) | \(\frac{1}{3}\) | \(0.333\) |
| \(-\frac{1}{2}\) | \(\frac{1}{\sqrt{3}}\) | \(0.577\) |
| \(0\) | \(1\) | \(1\) |
| \(\frac{1}{2}\) | \(\sqrt{3}\) | \(1.732\) |
| \(1\) | \(3\) | \(3\) |
| \(\frac{3}{2}\) | \(\sqrt{3^3}\) | \(5.196\) |
| \(2\) | \(9\) | \(9\) |
We will now plot these points on our graph, using a ruler to plot the decimal numbers as best as we can. We end up with something that looks like this:

We have plotted enough points to give us an idea of what the graph should look like. Joining up these points with as smooth a curve as possible, we get something like this:
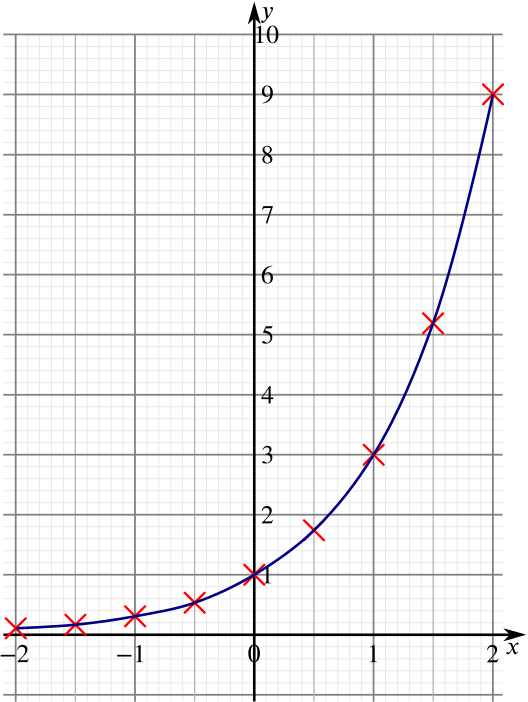
Use your graph to find
- the roots of the equation \(3^x=3x+2\)…
We can solve this using our sketch by drawing on the line \(y=3x+2\) and seeing where it intersects our sketch of \(y=3^x\). We choose two points on \(y=3x+2\) that are easy to plot and are far enough away from each other so that it doesn’t exaggerate any inaccuracies in our graph, and one between them just to be safe, \((-1,-1)\), \((0,2)\) and \((2,8)\). Drawing this line on top of our original sketch yields the following picture:
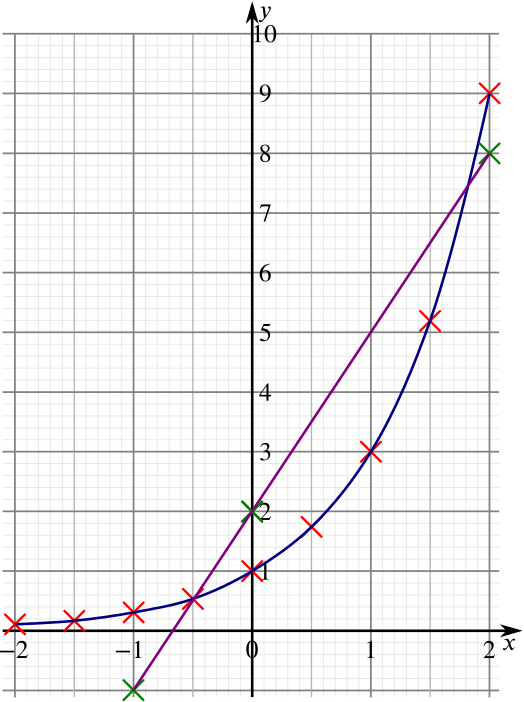
We can now see where these two graphs intersect, and reading off the appropriate values of \(x\) gives us the approximate solutions to \(3^x=3x+2\):
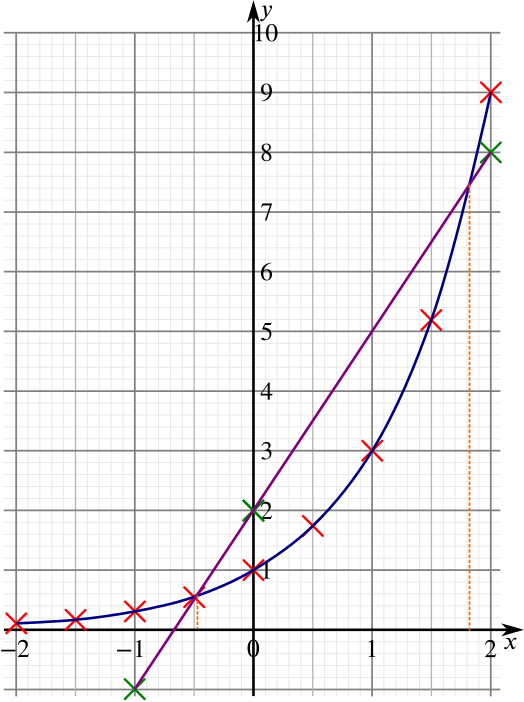
From the picture we have drawn here, it looks like we have \(x = -0.48\) and \(x = 1.83\) to two decimal places.
It turns out that the actual solutions are \(x=-0.4673...\) and \(x=1.8344...\), so we were close! How precise should we be with our answers?
Use your graph to find
- the range of values of \(k\) for which the equation \(3^x=kx\) has no real roots.
By drawing lines of the form \(y=kx\) on top of our original graph, that is, lines through the origin with any slope, we can see that if \(k\) is small enough then the line won’t intersect the graph of \(y=3^x\) at all, and so \(3^x=kx\) will have no real roots. Put your ruler on top of your sketch and pretend that the edge is a line through the origin. Start where it intersects \(y=3^x\) in two places and rotate it down, making sure it still passes through the origin. You should notice that just before the line stops intersecting \(y=3^x\), it touches the curve at just one point, as in the following picture:
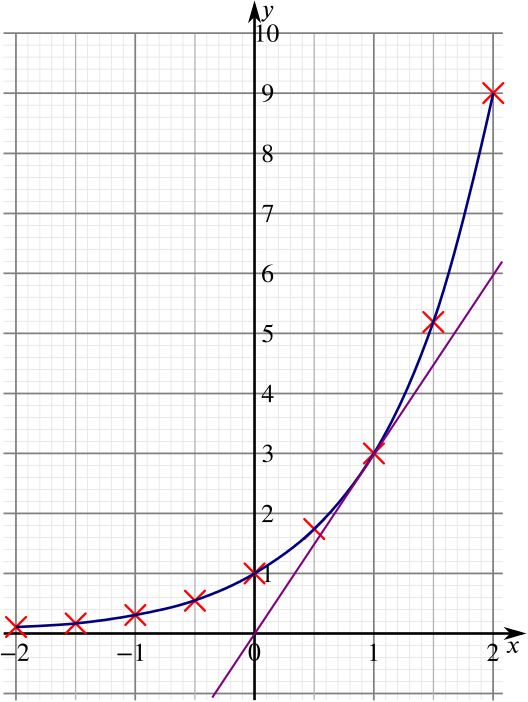
From the picture we can see that this line passes through \((0,0)\) and \((1,3)\) (approximately) and so has equation \(y=3x\) (approximately). So we have that \(3^x=kx\) has no real roots for any \(0\le k<3.0\) to one decimal place.

