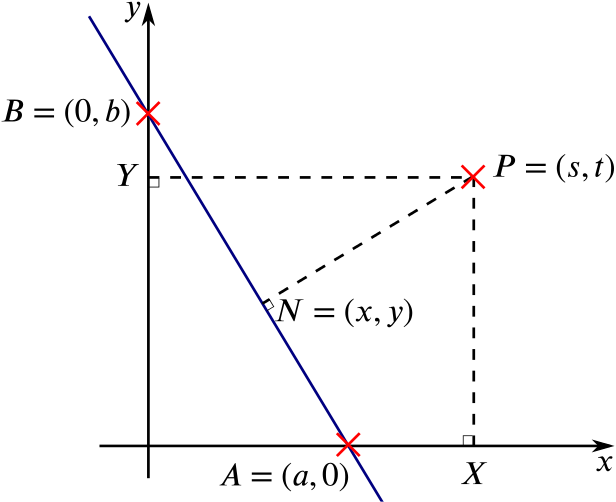
In the \(x\)–\(y\) plane, the point \(A\) has coordinates \((a,0)\) and the point \(B\) has coordinates \((0,b)\), where \(a\) and \(b\) are positive. The point \(P\), which is distinct from \(A\) and \(B\), has coordinates \((s,t)\). \(X\) and \(Y\) are the feet of the perpendiculars from \(P\) to the \(x\)-axis and \(y\)-axis respectively, and \(N\) is the foot of the perpendicular from \(P\) to the line \(AB\). Show that the coordinates \((x,y)\) of \(N\) are given by \[x = \frac{ab^2 - a(bt - as)}{a^2 + b^2}, \quad y = \frac{a^2b + b(bt - as)}{a^2 + b^2}.\]
Here’s a diagram of the situation.
You might also like to experiment with the situation in a more dynamic way using the GeoGebra applet here.
The gradient of the line \(AB\) is \(\frac{-b}{a}\), so the line has equation \(y=-\frac{b}{a}(x-a)\), which rearranges to \(bx+ay=ab\) or \(\frac{x}{a}+\frac{y}{b}=1\), which has a nice symmetry to it.
As the line \(AB\) has gradient \(-\frac{b}{a}\), it follows that the line perpendicular line \(NP\) has gradient \(\frac{a}{b}\). So \(NP\), passing through \(P(s,t)\) has equation \(y-t = \frac{a}{b}(x - s)\), which we can rearrange to get \(ax-by=as-bt\).
Now we know that \(AB\) and \(NP\) intersect at \(N\), so to find the coordinates of \(N\) we solve the simultaneous equations \[\begin{align} &&bx+ay&=ab\label{eq:1}&&\quad\\ \text{and}\quad&&ax-by&=as-bt.\label{eq:2} \end{align}\]Adding \(b\times\eqref{eq:1}\) to \(a\times\eqref{eq:2}\) gives \[(a^2+b^2)x=ab^2+a^2s-abt\] so \[x=\frac{ab^2+a^2s-abt}{a^2+b^2}=\frac{ab^2-a(bt-as)}{a^2+b^2}.\]
Similarly, subtracting \(b\times\eqref{eq:2}\) from \(a\times\eqref{eq:1}\) gives \[(a^2+b^2)y=a^2b-abs+b^2t\] so \[y=\frac{a^2b-abs+b^2t}{a^2+b^2}=\frac{a^2b+b(bt-as)}{a^2+b^2}\] as required.
Show that, if \[\left(\frac{t - b}{s}\right)\left(\frac{t}{s - a}\right) = -1,\] then \(N\) lies on the line \(XY\).
The points \(X\) and \(Y\) have coordinates \((s,0)\) and \((0,t)\) respectively, so by the same argument as for \(AB\), we see that the equation of the line \(XY\) is \[tx+sy = st.\]
Now \(N\) lies on this line exactly when \[\begin{align*} &t\frac{ab^2-a(bt-as)}{a^2+b^2} + s\frac{a^2b+b(bt-as)}{a^2+b^2}=st\\ \iff\quad& ab^2t-at(bt-as) + a^2bs + bs(bt-as) = st(a^2+b^2)\\ \iff\quad& ab^2t - abt^2 +a^2st + a^2bs + b^2st - abs^2 = a^2st + b^2st\\ \iff\quad& ab^2t - abt^2 + a^2bs - abs^2 = 0\\ \iff\quad& bt - t^2 + as - s^2 = 0\quad\text{as $ab$ is non-zero}\\ \iff\quad& t(b-t) + s(a-s) = 0. \end{align*}\]Then assuming that \(s\) and \(a-s\) are non-zero, we can divide by them to see that \(N\) lies on this line exactly when \[\frac{t(b-t)}{s(a-s)}+1=0,\] which is equivalent to the condition we were asked to show (and in fact stronger, as we have shown that this is also a necessary condition).
Give a geometrical interpretation of this result.
A geometrical interpretation of this result is that \(\dfrac{t - b}{s}\) and \(\dfrac{t}{s - a}\) are the gradients of \(BP\) and \(AP\) respectively. So if \(BP\) and \(AP\) are perpendicular, then \(N\) lies on \(XY\).
And what does this mean? We know that the angle in a semi-circle is a right angle.
So \(N\) lies on \(XY\) exactly when \(P\) lies on the circle with \(AB\) as diameter.
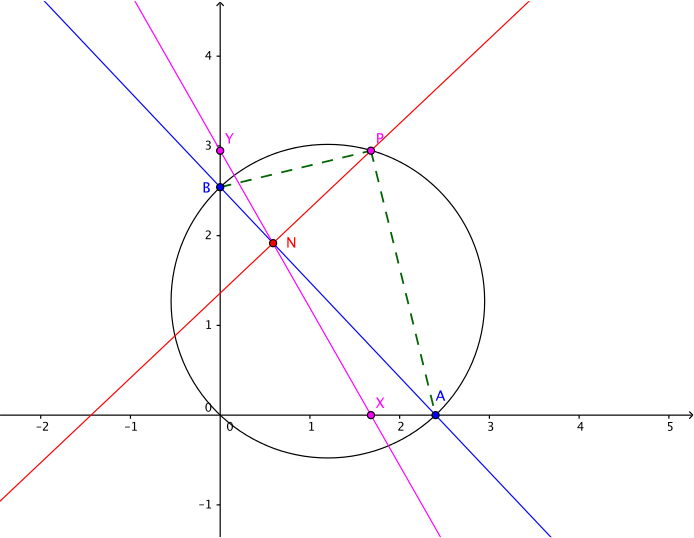
You can explore this further by showing the circle in the GeoGebra applet.

