From the inequalities \[y-2x>0,\qquad x+y>3,\qquad 2y-x<5\] deduce that \[\frac{1}{3}< x < \frac{5}{3},\qquad 2< y <\frac{10}{3}\]
Consider the three inequalities in the plane:
\(y-2x = 0\) crosses the axes at \((0,0)\) and has gradient \(2\) (it rearranges to \(y=2x\)). The region \(y-2x>0\) lies above this line, as it includes the point \((0,1)\).
\(x+y =3\) crosses the axes at \((0,3)\) and \((3,0)\). The region \(x+y>3\) lies above this line, as it does not include the point \((0,0)\).
\(2y-x =5\) crosses the axes at \((0,\frac52)\) and \((-5,0)\). The region \(2y-x<5\) lies below this line, as it includes the point \((0,0)\).
We can therefore sketch these three regions in the plane. Here the shaded regions are those which do not satisfy the inequality.
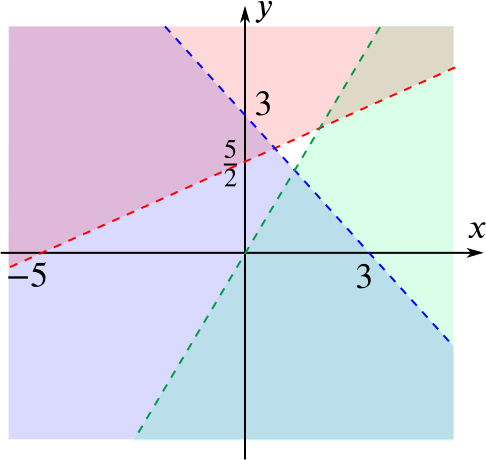
From these we can deduce the minumum and maximum extent of both \(x\) and \(y\): \[\frac{1}{3} < x < \frac{5}{3}, \qquad 2< y < \frac{10}{3},\] as required.
… and hence that the given inequalities cannot be satisfied simultaneously by integral values of \(x\) and \(y\).
The only integer value of \(x\) that satisfies \(\frac{1}{3} < x < \frac{5}{3}\) is \(x=1\).
The only integer value of \(y\) that satisfies \(2< y < \frac{10}{3}\) is \(y=3\).
Does the point \((1,3)\) obey all three inequalities simultaneously? \[\begin{align*} y-2x &> 0: \quad 3-2=1>0 \quad \checkmark \\ x+y &>3: \quad 1+3=4>3 \quad \checkmark \\ 2y-x &<5: \quad 6-1=5 \nless 5 \quad \mathsf{X} \end{align*}\]Thus there is no integer pair of \(x\) and \(y\) that satisfies all three inequalities simultaneously.

