Can we reflect this point in this line?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let \(L\) be the line with equation \(3x + 4y = 50\).

The point \(P(3,4)\) and its reflection \(P'\) in the line \(L\) are related in two ways: the line \(PP'\) is perpendicular to the line \(L\), and \(P\) and \(P'\) are equidistant (equal distances) from \(L\). (So in terms of vectors, \(\overrightarrow{PM}=\overrightarrow{MP'}\), where \(M\) is the point of intersection of \(PP'\) and \(L\).)

Now \(L\) has gradient \(-\frac{3}{4}\), so any line perpendicular to \(L\) will have gradient \(\frac{4}{3}\).

The perpendicular line \(PP'\) passing through \(P(3,4)\) therefore has equation \[y - 4 = \frac{4}{3}(x - 3),\] that is, \[y = \frac{4}{3}x.\]

From substituting this into the equation for \(L\), we see that \(L\) and \(PP'\) intersect at \(M\), where \[3x + 4 \times \frac{4}{3}x = 50,\] and rearranging this gives \[\frac{25}{3} x = 50,\] that is, \[x = 6.\] Then substituting this into either equation gives \(y = 8\), so \(M\) lies at \((6,8)\).

We must now use this information to find the reflected point. We can see that the difference in \(x\)-coordinates between \((3,4)\) and \((6,8)\) is \(3\), and the difference in \(y\)-coordinates is \(4\). So to get the reflected point \(P'\), we must add \(3\) to the \(x\)-coordinate and \(4\) to the \(y\)-coordinate of \(M(6,8)\), as illustrated below:

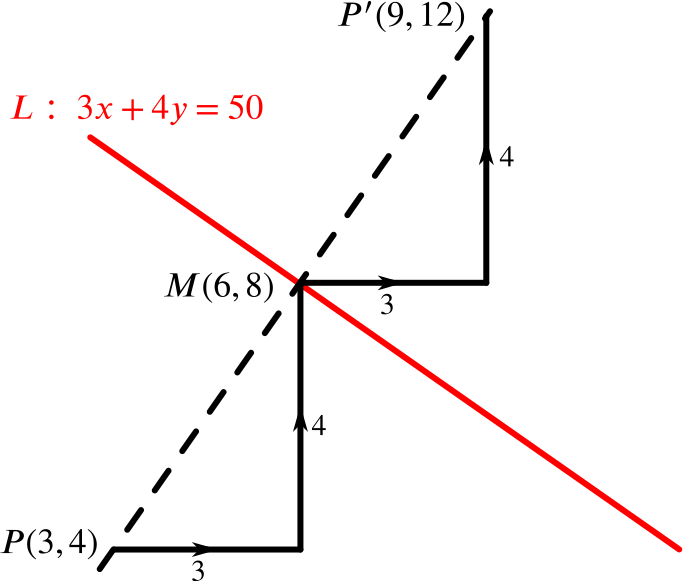
This tells us that the coordinate of the reflected point is \((9,12)\).

The answer is (a).