Three points have coordinates \(A(-2, -1)\), \(B(6, 9)\) and \(C(2, -3)\). The line through the midpoint of \(AB\) parallel to \(AC\) meets the \(x\)-axis at \(X\) and the \(y\)-axis at \(Y\). Calculate the coordinates of \(X\) and \(Y\).
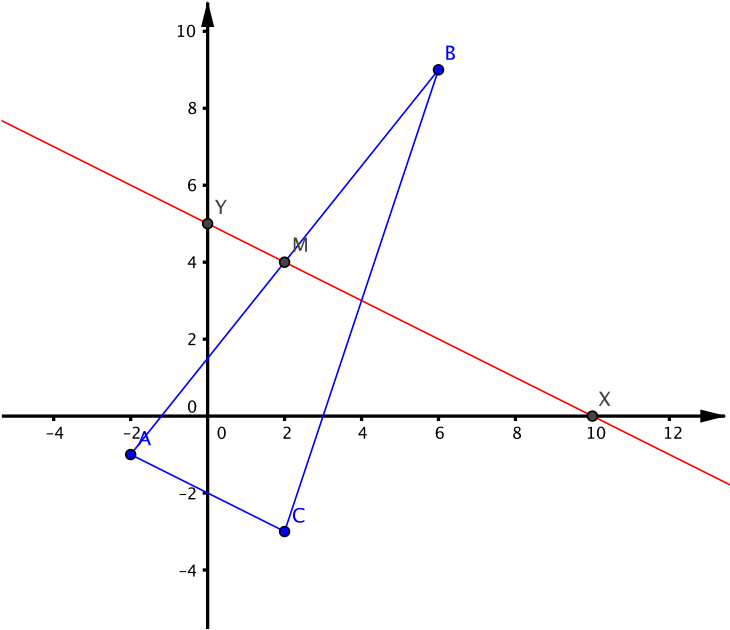
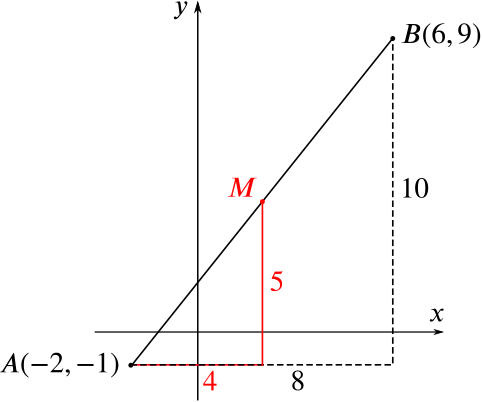
We will first find the midpoint of \(AB\); let’s call it \(M\).
The midpoint of \(AB\) has coordinates which are midway between the coordinates of \(A\) and \(B\).
So in general, given two points \(A(x_1, y_1)\) and \(B(x_2, y_2)\), the midpoint has coordinates \(\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\).
In this case, therefore, \(M\) has coordinates \(\left(\dfrac{-2 + 6}{2}, \dfrac{-1 + 9}{2}\right) = (2, 4)\).
What is the equation of the line through \(M\) parallel to \(AC\)? We will use the fact that two lines are parallel if and only if they have the same gradient.
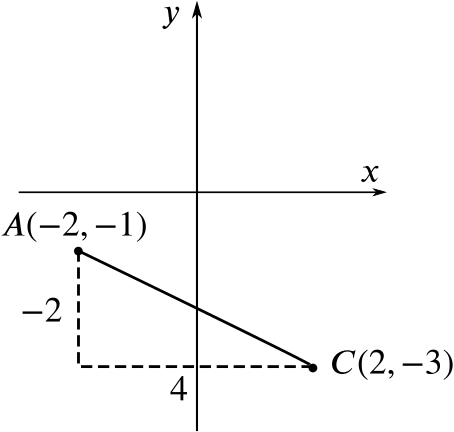
The gradient of the line \(AC\) is \(\dfrac{-3-(-1)}{2-(-2)}=\dfrac{-2}{4} = - \dfrac{1}{2}\). So the line through \(M\) parallel to \(AC\) has gradient \(-\dfrac12\).
As it passes through \(M(2,4)\), it therefore has equation \(y-4=-\frac12(x-2)\) (using the general formula \(y-y_1=m(x-x_1)\)), which rearranges to \(y=-\frac12 x+5\).
We now want to find \(X\) and \(Y\), which are the intercepts with the \(x\) and \(y\) axes respectively.
To find \(X(x,0)\), we solve the equation \(0 = -\dfrac{1}{2} x + 5\), and therefore we have \(X=(10, 0)\).
To find \(Y(0,y)\), we solve \(y = -\dfrac{1}{2} \times 0 + 5\), which gives \(y = 5\). Therefore, \(Y\) has coordinates \((5, 0)\).
Hence deduce the area of \(\triangle XOY\), where \(O\) is the origin.
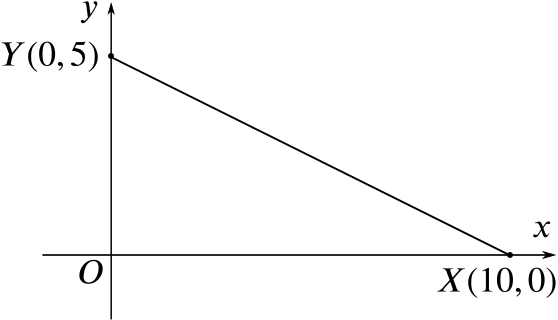
The triangle \(\triangle XOY\) is right-angled, so its area is given by \(\frac12 OX\times OY=\frac 12\times 10\times 5=25\).