In Fig. 1 (not drawn to scale) the curve has equation \(x^2+4y^2=16\). The straight line has a gradient of \(-2\) and passes through the intersection of the curve with the positive \(y\)-axis.
Write down the three inequalities which are sufficient to define the shaded area (including the three lines bounding it).
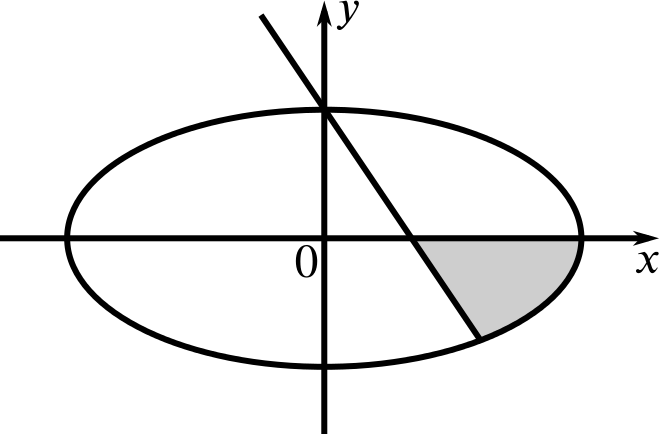
Since the shaded area is inside the curve, the first inequality is \[x^2+4y^2\le 16.\] (We can check the direction of the inequality by testing with a point in the inside, say \((0,0)\). This gives \(0^2+4\times0^2=0\le 16\), so we have our inequality the correct way round.)
Since the shaded area is below the \(x\)-axis, the second inequality is \[y\le 0.\]
The third inequality will relate to the straight line, which we know must be of the form \(y=c-2x\). To find \(c\), we must first find where the curve crosses the positive \(y\)-axis.
When \(x=0\), \(4y^2=16\), and so \(y=\pm2\). Since we wish to know where the curve crosses the positive \(y\)-axis, this point is \((0,2)\) (so the \(y\)-intercept is 2).
Putting this point into the equation of the line (or by knowing the \(y\)-intercept), we find that \(c=2\), and so the equation of the line is \(y=2-2x\).
Since the shaded area is above the line, the third inequality is \[y\ge 2-2x.\]

