In Fig. 1 (not drawn to scale) the curve has equation \(x^2+4y^2=16\). The straight line has a gradient of \(-2\) and passes through the intersection of the curve with the positive \(y\)-axis.
Write down the three inequalities which are sufficient to define the shaded area (including the three lines bounding it).
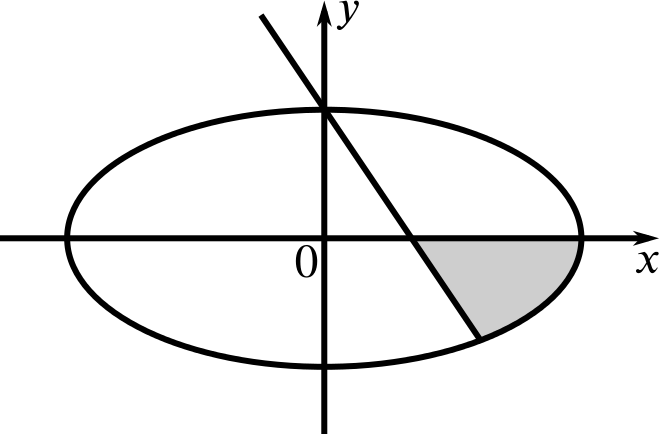
Should the inequalities be of the form \(y \leq f(x)\) or \(y \geq f(x)\)? Or are there other useful ways to write inequalities?
If you’re not sure which way round an inequality should go, choose a point not on the boundary; does it have coordinates that make the inequality work? If so, the point is on the side you want.

