The diagram shows the ellipse whose equation is \(x^2+y^2-xy+x-4y=12\). The curve cuts the \(y\)-axis at points \(A\) and \(C\) and cuts the \(x\)-axis at points \(B\) and \(D\). What is the area of the inscribed quadrilateral \(ABCD\)?
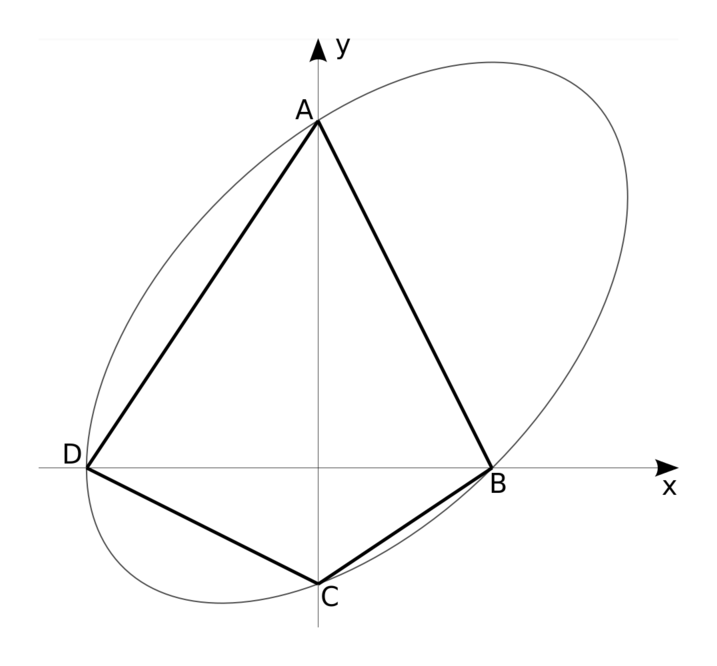
If we know the coordinates of the four points \(A\), \(B\), \(C\) and \(D\), then we can split the quadrilateral into two triangles, \(ABD\) and \(BCD\). Using the coordinates, we can find the base (\(BD\)) of these triangles and their heights (\(OA\) and \(OC\), where \(O\) is the origin). We can therefore find their areas and add them to obtain the area of \(ABCD\).
The areas of the triangles are \(\frac12 BD\times OA\) and \(\frac12 BD\times OC\); if we add these together, we obtain \(\frac12 BD(OA+OC)=\frac12 BD\times AC\) for the area of the quadrilateral, that is, half of the product of the diagonals.
This formula is true for any quadrilateral with perpendicular diagonals. Can you see why? Is it true even if the quadrilateral is not convex?
At the points \(A\) and \(C\) we have \(x=0\), so the \(y\)-coordinate must satisfy \(y^2-4y-12=0\), that is, \(y=6\) or \(y=-2\). So from the diagram, we see that \(A=(0,6)\) and \(C=(0,-2)\).
Similarly, we have \(y=0\) at the points \(B\) and \(D\) and so \(x^2+x-12=0\), that is, \(x=3\) or \(x=-4\). Therefore using the diagram, we get \(B=(3,0)\) and \(D=(-4,0)\).
Therefore the triangle \(ABD\) has area \(\frac12\times7\times6=21\) and \(BCD\) has area \(\frac12\times7\times2=7\), and so the quadrilateral has area \(21+7=28\).

