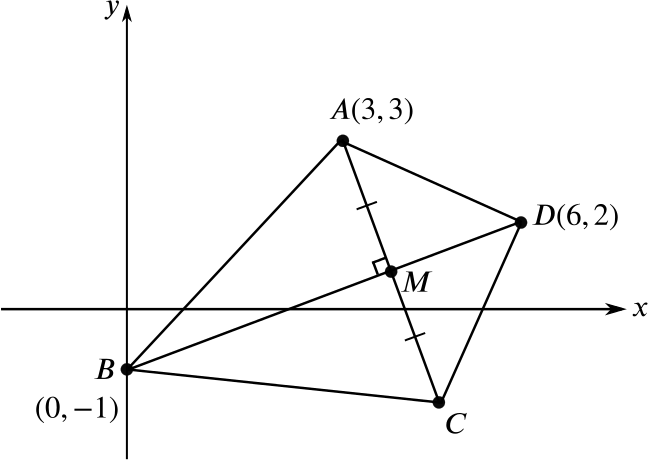
In the quadrilateral \(ABCD\), the points \(A\), \(B\) and \(D\) are at \((3, 3)\), \((0, -1)\) and \((6, 2)\) respectively. The line \(BD\) bisects the line \(AC\) at right angles at the point \(M\). Find the equation of \(BD\) and of \(AC\).
Remember what the connections between the lines \(AC\) and \(BD\) are. How can you use this?
Calculate
- the coordinates of \(M\),
- the coordinates of \(C\),
Can you make use of part (i) when answering part (ii)?
- the area of the quadrilateral \(ABCD\).
How can we break \(ABCD\) into shapes whose areas we do know how to calculate?

