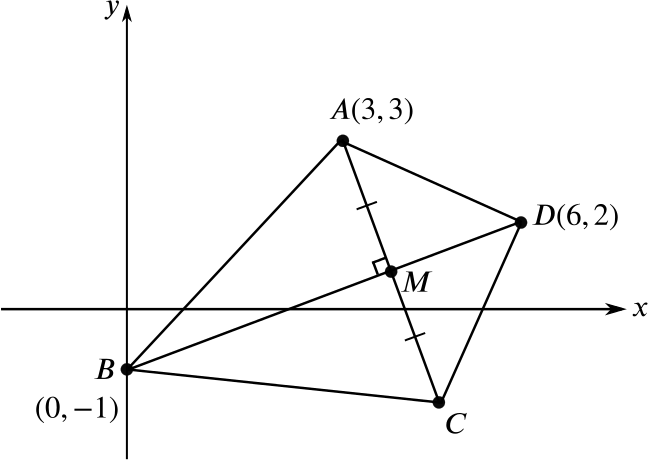
In the quadrilateral \(ABCD\), the points \(A\), \(B\) and \(D\) are at \((3, 3)\), \((0, -1)\) and \((6, 2)\) respectively. The line \(BD\) bisects the line \(AC\) at right angles at the point \(M\). Find the equation of \(BD\) and of \(AC\).
Let us first find the equation of the line \(BD\). The gradient of the line is \(\dfrac{2-(-1)}{6} = \dfrac{1}{2}\). Thus the equation of the line is of the form \(y = \frac{1}{2}x + c\), where \(c\) is the \(y\)-axis intercept. But we know that the line intersects the \(y\)-axis at \(y = -1\) and hence the equation of the line \(BD\) is \[y = \tfrac{1}{2}x - 1.\]
In order to find the equation of the line \(AC\) recall that the lines \(AC\) and \(BD\) are perpendicular to each other. Hence the gradient of the line \(AC\) is \(-2\). Since the point \(A(3,3)\) lies on \(AC\), the equation of the line is \(y-3=-2(x-3)\) (using the general formula \(y-y_1=m(x-x_1)\)). We can rearrange this to get \[y = -2x + 9.\]
Calculate
- the coordinates of \(M\),
The point \(M\) is given by the intersection of the two lines \(AC\) and \(BD\). Let us therefore solve the equation \[\frac{1}{2}x - 1 = -2x + 9.\] This is equivalent to the equation \(\frac{5}{2}x = 10\) which gives \(x = 4\). Now we can use the equation of either of the two lines to compute the \(y\)-coordinate to be \(y = -2 \times 4 + 9 = 1\). Hence the coordinates of the point \(M\) are \((4, 1)\).
- the coordinates of \(C\),
Recall that the line \(BD\) bisects the line \(AC\). Hence the line \(AM\) has the same length as the line \(MC\). Consider the following diagram.
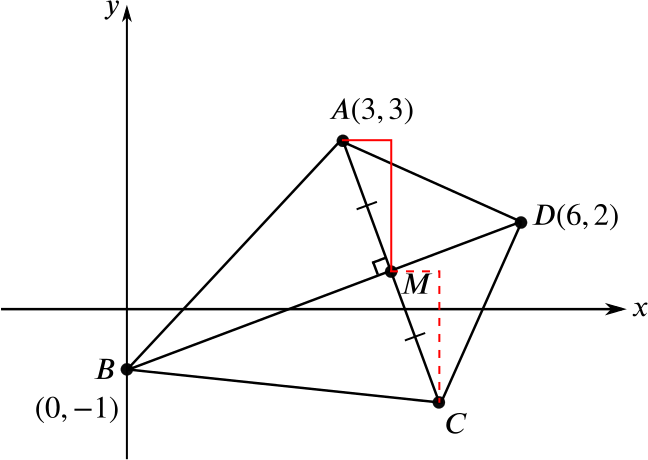
In order to go from \(A\) to \(M\), we have to go one unit to the right and two units down. Hence in order to find the coordinates of \(C\) we have to start at \(M\) and go one unit to the right and two units down. Thus the coordinates of \(C\) are \((5, -1)\).
We can express this in terms of vectors. The last paragraph could be rewritten: We see that \(\overrightarrow{AM}=\overrightarrow{MC}=\dbinom{1}{-2}\), and hence \(C\) has coordinates \((5,-1)\).
- the area of the quadrilateral \(ABCD\).
We could split the quadrilateral \(ABCD\) into the four triangles \(ABM\), \(BCM\), \(CDM\), and \(DAM\), and compute their areas separately now that we know the coordinates of each of the points involved. Alternatively, we could split it into the two triangles \(BAD\) and \(BCD\) and work out the areas of these. We could also use the result that the area of a kite equals half the product of its diagonals, so that the area is \(\frac12 AC\times BD\).
In order to do any of these, we will have to use the Pythagorean Theorem to work out the lengths involved (the base and height of each triangle or the lengths of the diagonals).
Let us instead offer an approach that does not use the Pythagorean Theorem at all.
Now that we know that \(B\) and \(C\) have the same \(y\)-coordinate, we can redraw the diagram so that \(BC\) is horizontal. Consider, then, the red rectangle in the following picture.
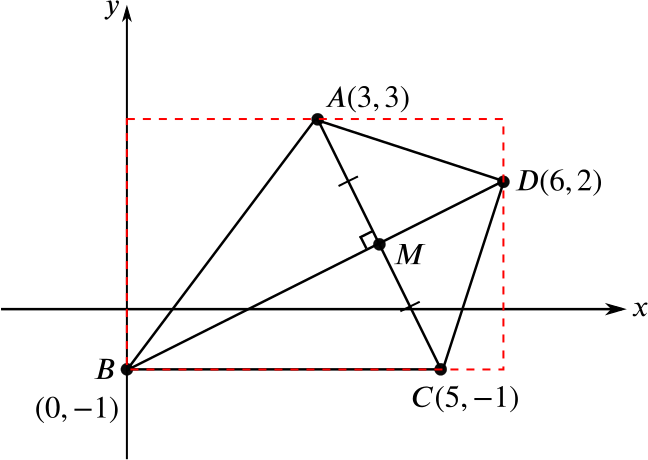
If we subtract the areas of the three triangles in the top left, top right, and bottom right corners of the rectangle from the area of the rectangle itself we get the area of the quadrilateral \(ABCD\). Notice that all three of these triangles are right-angled and we can easily work out the lengths of the sides enclosing the right angle.
The rectangle has height \(4\) and width \(6\) and thus an area of \(4 \times 6 = 24\).
The triangle in the top left corner has sides of length \(4\) and \(3\), hence it has an area of \(\frac12\times 4 \times 3 = 6\). Similarly, the triangle in the top right corner has sides of length \(3\) and \(1\) and hence an area of \(\frac{3}{2}\). The triangle in the bottom right corner has sides of length \(1\) and \(3\) and therefore also has an area of \(\frac{3}{2}\). In total, the area of the quadrilateral \(ABCD\) is therefore \[24 - 6 - \tfrac{3}{2} - \tfrac{3}{2} = 15.\]

