The largest possible value of \(x\) is
\(6\),
\(7\),
\(8\),
\(9\).
A graphical approach
First, we sketch the three lines \[\begin{align*} 2x+3y &= 23, \\ x+2 &= 3y\quad\text{and}\\ 3y+1 &=4x, \end{align*}\]by rearranging them in the form \(y=mx+c\) first.
Then thinking about which side of each of the lines is satisfied by the inequalities, we see that the central triangular region is the one satisfied by all three inequalities.
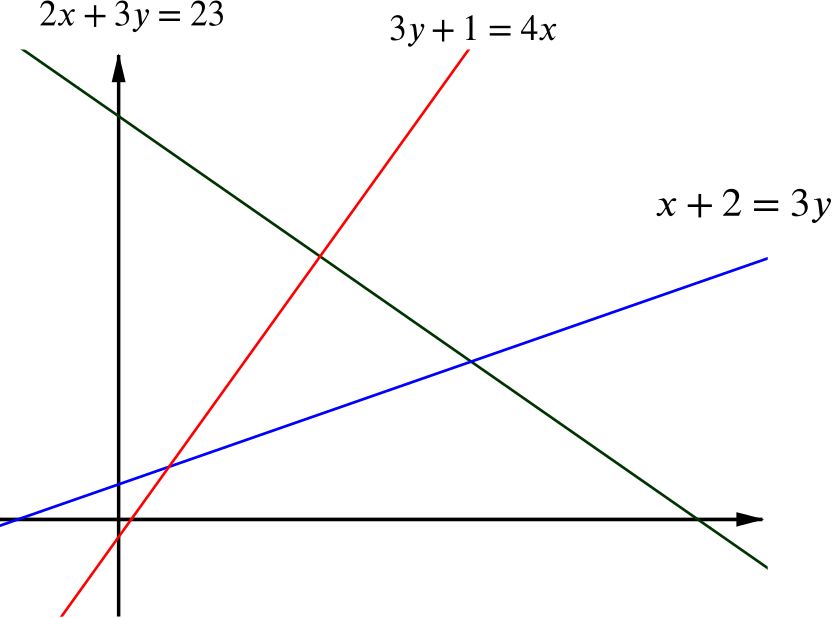
We can see from the graph that the largest possible value of \(x\) is where the lines \(2x+3y=23\) and \(x+2=3y\) intersect, which is at the point \((7,3)\).
So the answer is (b).
An algebraic approach
We want to find the largest possible value of \(x\), so we aim to eliminate \(y\).
First attempt:
The third inequality rearranges to give \(3y\le 4x-1\).
We cannot substitute this into the first inequality, as the directions of the inequalities are not compatible.
If we substitute it into the second inequality, though, we obtain \(x+2\le 4x-1\), so \(3x\ge3\), or \(x\ge1\), which is not so helpful.
Second attempt:
The first inequality rearranges to give \(3y\le 23-2x\). Combining this with the second inequality gives \[x+2\le 3y\le 23-2x\] so \(3x\le 21\) or \(x\le7\).
If \(x=7\), the second inequality gives \(9\le 3y\), so we could try \(y=3\). This pair of values satisfies all three inequalities, so the greatest possible value of \(x\) is \(7\), and the answer is (b).

