We graphed the following three pairs of equations, all on the same axes.
\(x + y - 1 = 0\) and \((x + y - 1)(x^2 + y^2) = 0\)
\(x + y = 0\) and \((x + y)(y^2 + (x+1)^2) = 0\)
\(x + y = 1\) and \(x^3 + 3xy + y^3 = 1\)
To our surprise, we could only see two lines on the graph.
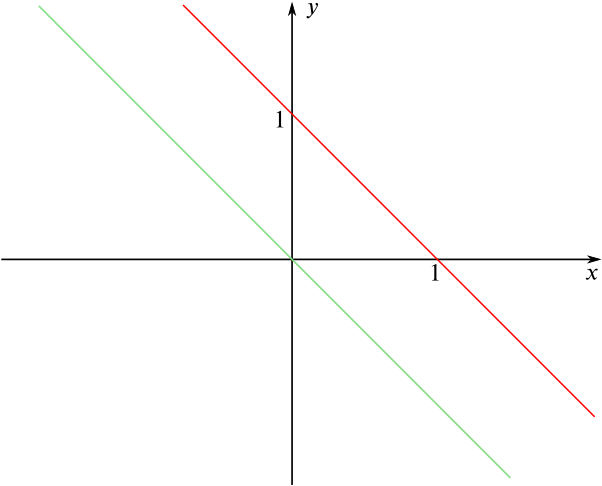
(You might also like to look at the graphs on Desmos.)
What has happened? Can you work out which equations go with which lines? Are there any points missing from the graph? If so, where should they be?
A point \((x,y)\) satisfies the equation \(x + y - 1 = 0\) if and only if it lies on the straight line with gradient \(-1\) passing through the point \((0, 1)\), and indeed we see that line on the picture.
A point \((x,y)\) satisfies the equation \((x + y - 1)(x^2 + y^2) = 0\) if and only if \(x + y - 1 = 0\) or \(x^2 + y^2 = 0\). So we get the same straight line as before, together with the solutions to \(x^2 + y^2 = 0\). But \(x^2 \geq 0\) and \(y^2 \geq 0\), so we see that the only solution is \((0,0)\). This shows that the equation \((x + y - 1)(x^2 + y^2) = 0\) corresponds to the straight line with gradient \(-1\) passing through the point \((0,1)\), together with the origin \((0,0)\).
It is rather hard to tell whether the origin is included for this equation in the graph above!
A point \((x,y)\) satisfies the equation \(x + y = 0\) if and only if it lies on the straight line with gradient \(-1\) through the origin, and we see that line on the picture.
A point \((x,y)\) satisfies the equation \((x + y)(y^2 + (x + 1)^2) = 0\) if and only if \(x + y = 0\) or \(y^2 + (x+1)^2 = 0\). So we get the same straight line with gradient \(-1\) through the origin, together with the solutions to \(y^2 + (x+1)^2 = 0\). Rather than multiplying out this expression, we can notice that \(y^2 \geq 0\) and \((x+1)^2 \geq 0\), so the only solution is \(x+1 = 0\) and \(y = 0\). This shows that the equation \((x + y)(y^2 + (x+1)^2) = 0\) corresponds to the straight line with gradient \(-1\) passing through the origin, together with the point \((-1,0)\).
We can rearrange the first equation of the third pair to make it the same as the first equation of the first pair, so we already know the points that satisfy this equation: they are precisely the points on the line with gradient \(-1\) passing through \((0,1)\).
Previously, the second equation in each pair has been in a factorised form, which has meant that we could read off the solutions. Inspired by our success there, we could try to factorise the second equation in the third pair to see whether we can use a similar strategy.
We have \(x^3 + 3xy + y^3 - 1 = (x + y - 1)(x^2 - xy + y^2 + x + y + 1)\), so the point \((x,y)\) satisfies the second equation in the third pair if and only if \((x + y - 1)(x^2 - xy + y^2 + x + y + 1) = 0\). We have already thought about \(x + y - 1 = 0\), so we concentrate on the equation \(x^2 - xy + y^2 + x + y + 1 = 0\).
Again we think about what worked for us last time: it was helpful to write our function as a sum of squares. Let’s see whether we can do the same thing again.
We have \(x^2 - xy + y^2 + x + y + 1 = \frac{1}{2}(x+1)^2 + \frac{1}{2}(y+1)^2 + \frac{1}{2}(x-y)^2\). This is a sum of squares, which are all non-negative, so the only way it can be zero is if every term is zero. This happens if and only if \(x = -1\), \(y = -1\), and \(x = y\).
We are looking for real solutions, so we need the part under the square root to be non-negative, but \(-3(y+1)^2 \leq 0\), with equality if and only if \(y = -1\). So the only way we might get a solution is if \(y = -1\), and we see that this then leads to \(x = -1\).
Fortunately, this agrees with our answer above from considering the expression as a sum of squares!
We have shown that the equation \(x^3 + 3xy + y^3 - 1 = (x + y - 1)(x^2 - xy + y^2 + x + y + 1) = 0\) corresponds to the straight line with gradient \(-1\) passing through the point \((0, 1)\), together with the single point \((-1,-1)\).

