Following on from problem 1, we have two fixed points \(A\) and \(B\) in the plane with \(AB=2a\), where \(a>0\).
A point \(P\) moves in the plane so that \[\frac{PA}{PB}=\lambda,\] where \(\lambda>0\).
We shall now assume that \(\lambda\ne1\), so that the locus of \(P\) is a circle.
What is the length of the tangent to this circle from the mid-point of \(AB\), that is, the length \(MN\) in the image below?
The radius and centre of the circle were found in the solution to problem 1.
This image shows the situation described in the case \(\lambda=2\), where a coordinate system has been imposed and the line \(CN\) has been drawn in.
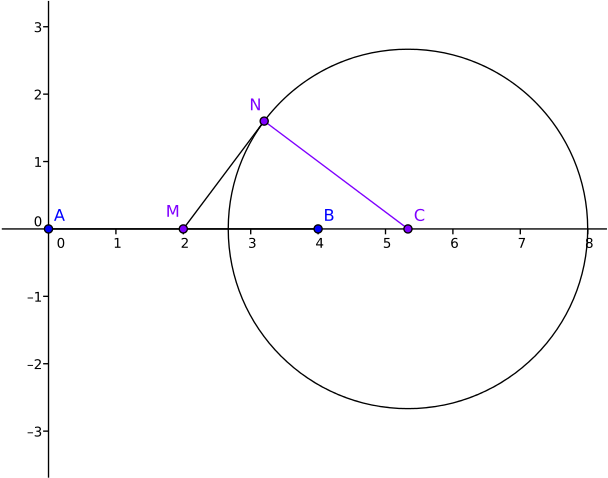
Incidentally, there are actually two tangents from \(M\) to the circle, but their lengths are equal. (Can you prove this?) We have only drawn one of them.
We note first that the tangent at \(N\) is perpendicular to the radius at \(N\), so the triangle \(CMN\) is right-angled. We can therefore use Pythagoras’s Theorem: \[CM^2=CN^2+MN^2.\]
Since we know the coordinates of \(C\) from the first part of the problem and \(M\) is the midpoint of \(AB\), we can easily work out the length \(CM\). The length \(CN\) is the known radius of the circle, and so we can deduce the length \(CM\).
We use the nice coordinates approach from the first solution to perform our calculations: \(A\) is at \((0,0)\) and \(B\) is \((2a,0)\), as in the diagram above. Then \(C\) is \(\left(\dfrac{2\lambda^2 a}{\lambda^2-1}, 0\right)\) and the circle has radius \(\dfrac{2\lambda a} {|\lambda^2-1|}\).
The midpoint \(M\) has coordinates \((a,0)\), so \[\begin{align*} MN^2&=CM^2-CN^2\\ &=\left(\frac{2\lambda^2 a}{\lambda^2-1}-a\right)^2- \left(\frac{2\lambda a} {|\lambda^2-1|}\right)^2\\ &=\left(\frac{(\lambda^2+1)a}{\lambda^2-1}\right)^2- \left(\frac{2\lambda a}{\lambda^2-1}\right)^2\\ &=\frac{(\lambda^4+2\lambda^2+1)a^2-4\lambda^2a^2}{(\lambda^2-1)^2}\\ &=\frac{(\lambda^4-2\lambda^2+1)a^2}{(\lambda^2-1)^2}\\ &=a^2. \end{align*}\]Therefore \(MN=a\), which is \(\frac{1}{2}AB\), independent of the choice of \(\lambda\)!
What is the locus of \(N\) as \(\lambda\) varies?
As \(MN=a\) is a constant and \(M\) is fixed, it follows that the locus of \(N\) as \(\lambda\) varies is (part of) the circle with diameter \(AB\), which is very pretty.
Which parts of this circle are included in the locus of \(N\) as \(\lambda\) varies? Are there any parts which are not?

