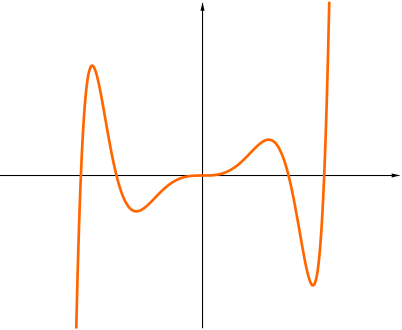
An odd function is a function \(f(x)\) with the property that \(f(-x)=-f(x)\) for any value of \(x\). The graph of \(y=f(x)\) for an odd function has rotational symmetry about the origin.
Examples are \(\sin x\) and \(x^3\).
Note that it is possible for a function to be neither odd nor even, for example \(f(x)=1+2x\).

