How can we find the length of a curve?
More precisely, if we have the graph of a function \(y=f(x)\), how can we find the length of the graph between \(x=a\) and \(x=b\), as shown in this sketch?
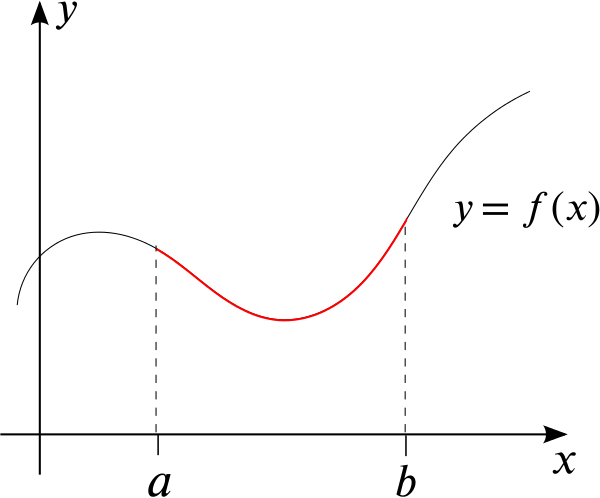
And if we have a curve given parametrically as \((x(t), y(t))\), how can we find the length of the curve between \(t=a\) and \(t=b\), as shown in the following sketch?
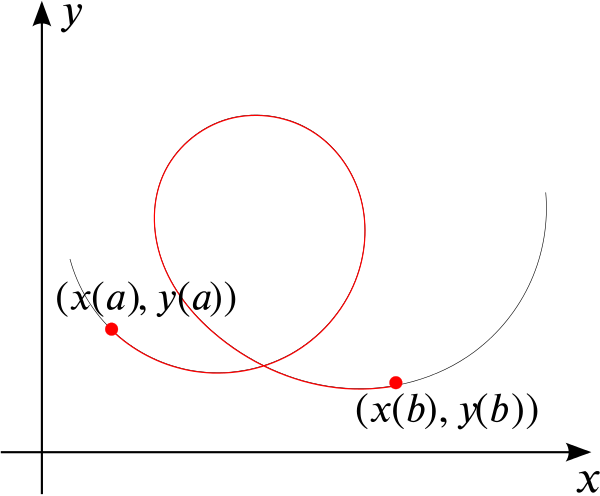
If you would like some guidance, have a look at the Structured prompts section.
Once you have general techniques for answering the above questions, have a go at these problems:
Find the length of the curve described parametrically by \(x=a\cos t\), \(y=b\sin t\) from \(t=0\) to \(t=\theta\). Where have you met this result before?
Find the length of the curve \(y=a\cosh\dfrac{x}{a}\) from \(x=0\) to \(x=x_0\). (This curve is called a catenary, and this result is closely related to some of the other resources at this station.)

