How long is a piece of string?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

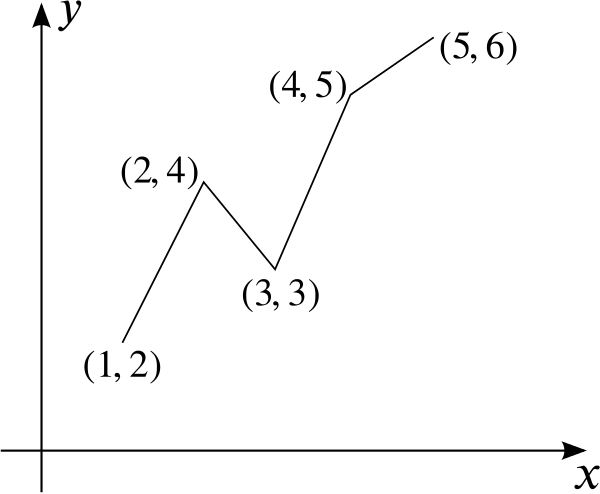
1. What is the length of this line (not drawn accurately)?

   

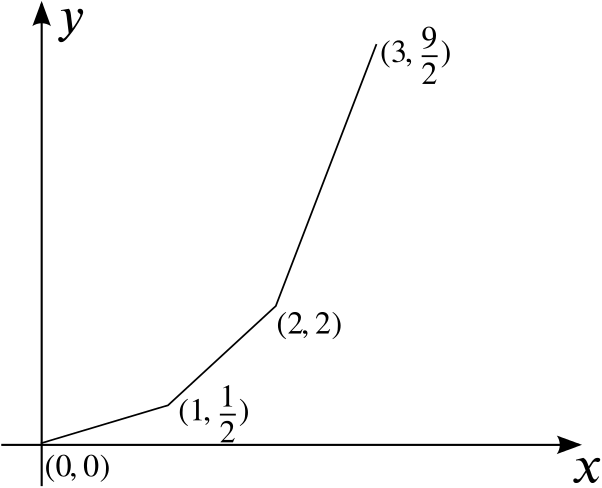
2. What about the length of this approximation to \(y=\frac{1}{2}x^2\) from \(x=0\) to \(x=3\) (again not drawn accurately)?

   

3. How could we get a better approximation to the length of \(y=\frac{1}{2}x^2\) from \(x=0\) to \(x=3\)?

4. How can you extend your answer to work out an expression for the exact length of \(y=\frac{1}{2}x^2\) from \(x=0\) to \(x=3\)?

   (Feel free to leave the expression in an unevaluated form if you do not know how to evaluate it.)

5. Extend this idea to answer the first main problem:

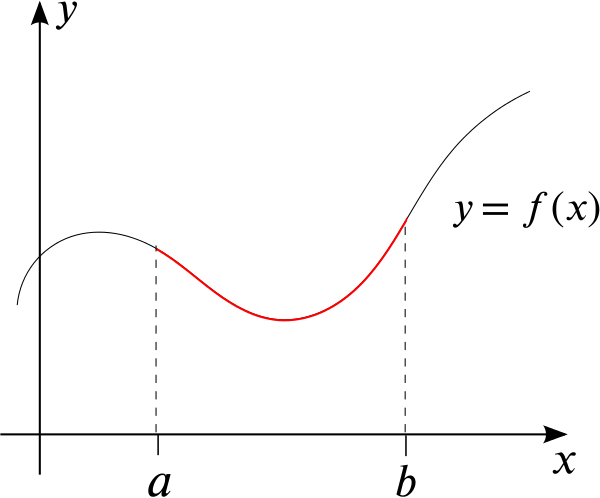
   More precisely, if we have the graph of a function \(y=f(x)\), how can we find the length of the graph between \(x=a\) and \(x=b\), as shown in this sketch?

   

6. Can you now extend your ideas to answer the second main problem?

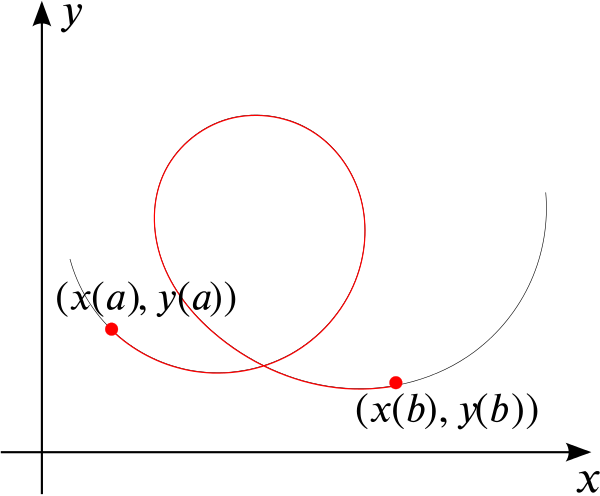
   And if we have a curve given parametrically as \((x(t), y(t))\), how can we find the length of the curve between \(t=a\) and \(t=b\), as shown in the following sketch?

   

With these answered, you should be able to tackle the two examples on the main problem page.