(This resource is still in draft form.)
This applet shows a square with slide length \(2\) rolling over an upside-down catenary with equation \(y=-\cosh x\). When the square is horizontal, the centre of its base touches the vertex of the catenary.
Move the slider to roll the square.
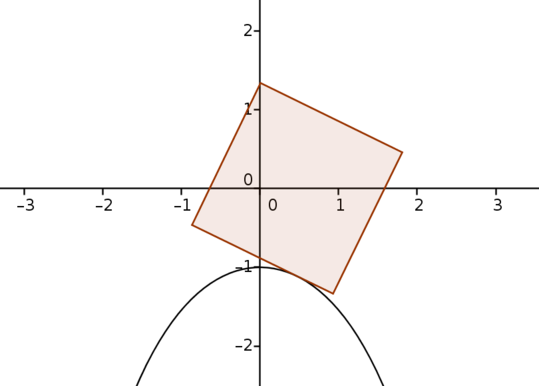
Brief solutions (require more detail):
What is the locus of the centre of the square?
The locus of the centre of the square is a straight line along the \(x\)-axis.
How far can the square roll with the same side still touching the catenary?
The square can rotate until the vertex of the square touches the catenary. At this point, the arc length of the catenary from the vertex of the catenary to this point equals half of the square’s side length, which is \(1\). The arc length from \((0,-1)\) to \((x, -\cosh x)\) is \(\sinh x\), so this occurs when \(\sinh x=1\), or \(x=\arsinh 1\). Using the formula for \(\arsinh\) or solving \(\sinh x=1\) directly gives an alternative expression for this: \(x=\ln(1+\sqrt{2})\).
Furthermore, at this point, the gradient of the catenary is \(y'=-\sinh x=-1\). This means that the square has rotated by \(45^\circ\), and thus the centre of the square is also at \(x=\arsinh 1\).

