(This resource is still in draft form.)
This applet shows a square with slide length \(2\) rolling over an upside-down catenary with equation \(y=-\cosh x\). When the square is horizontal, the centre of its base touches the vertex of the catenary.
Move the slider to roll the square.
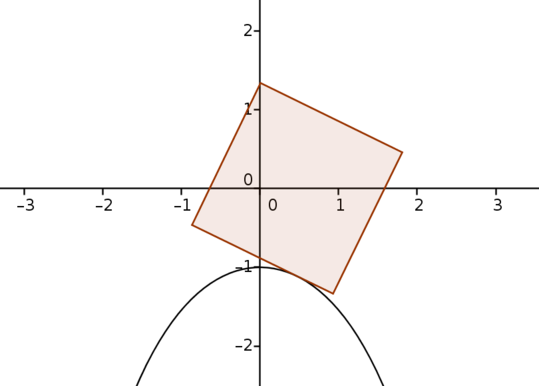
What is the locus of the centre of the square?
How far can the square roll with the same side still touching the catenary?
What do you already know about catenaries?
When the square has turned a certain amount, what are some different ways in which you could describe its location?

