Consider the shaded area under each function shown on the cards.
Put the cards in order of size of the shaded area, from smallest to largest.
(a)
(b)
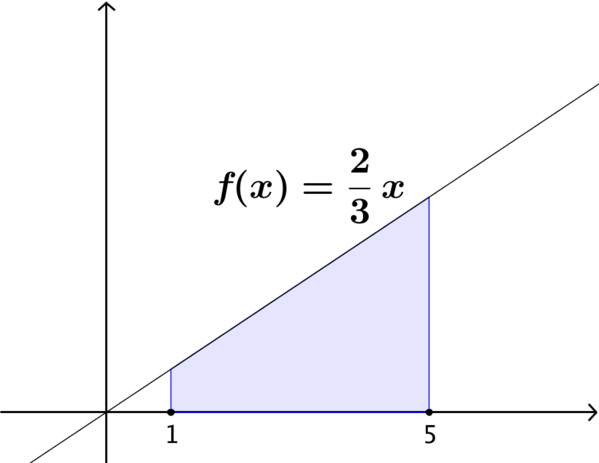
(c)
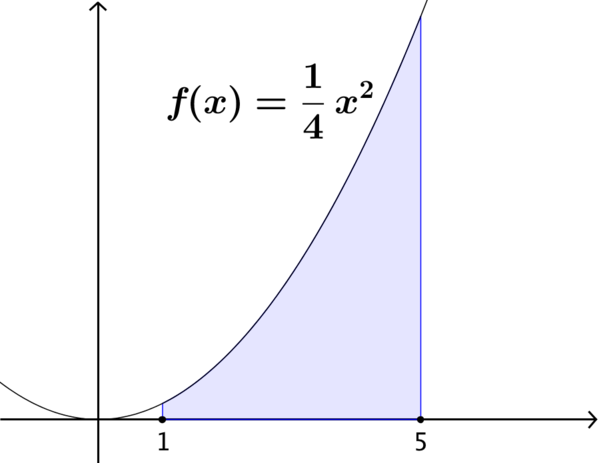
(d)
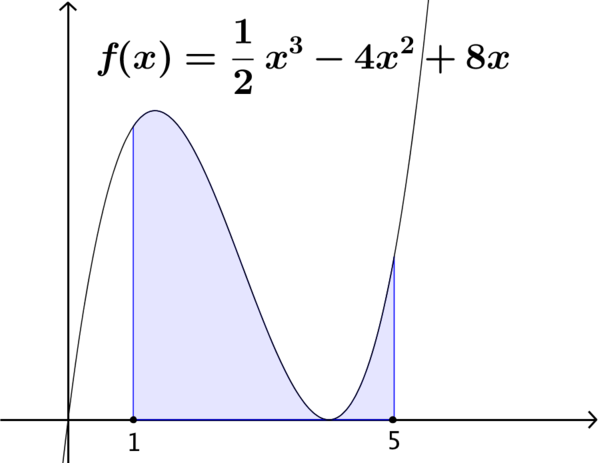
How did you decide which card has the smallest shaded area? What about the largest?
The exact value for the area under each function, in order of increasing size, is:
Card
Function
Area
\(f(x)=\dfrac{2}{3}x\)
\(8\)
\(f(x)=\dfrac{1}{2}x^3-4x^2+8x\)
\(\dfrac{26}{3}\)
\(f(x)=\dfrac{1}{4}x^2\)
\(\dfrac{31}{3}\)
\(f(x)=\dfrac{11}{4}\)
\(11\)
How close were your estimates to these exact values? Were they over or under-estimates?
How could you have improved these estimates?
How can you refine your methods of estimating the areas under the quadratic and cubic curves to obtain answers that are correct to \(1\) decimal place?
