What can you say about the area under each function on the two cards below, between \(x=1\) and \(x=2\)?
Which is greater?
|
(a) \[f(x)=\left(4-x^2\right)^{\frac{1}{2}}\] |
(b) 
|
Card (a)
The given function represents a semi-circle of radius \(2\), centred on the origin. The area we are concerned with is shaded in purple.
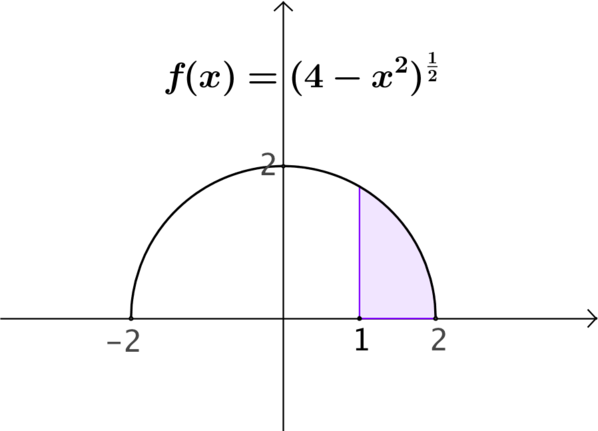
Cards (a) & (b)
It makes sense to begin our comparison by plotting the two functions on the same axes. Based on our subsequent observations we can think about accuracy and perhaps consider alternative approaches as a comparison.
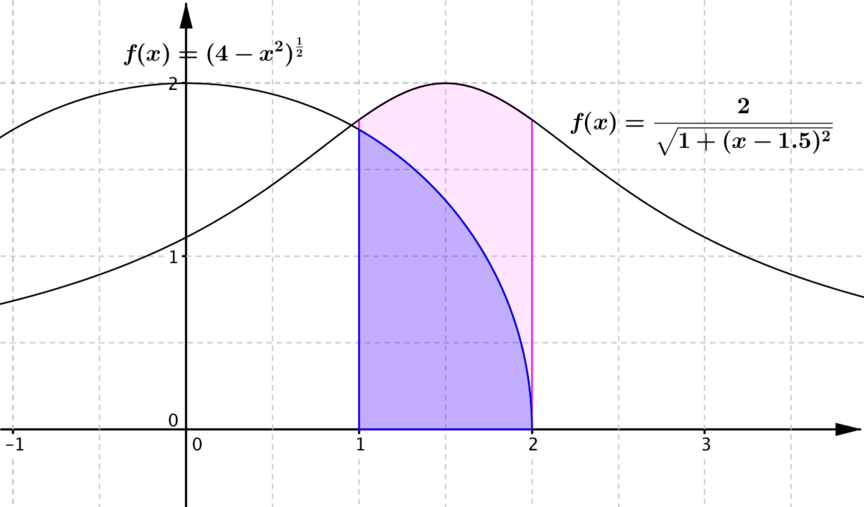
How can you convince someone that the maximum value of each function is the same?
What can you say about the area under each function on the two cards between \(x=1\) and \(x=2\)?
The maximum value of \(f(x) = \dfrac{2}{\sqrt{1 + (x - 1.5)^2}}\) will occur when the denominator, \(\sqrt{1+(x-1.5)^2}\), is at a minimum.
The expression inside the square root cannot take a value less than \(1\) and the minimum value will occur when \((x - 1.5)^2 = 0\), corresponding to \(x = 1.5\).
Substituting this value of \(x\) into the function we have \[f(1.5) = \frac{2}{\sqrt{1}} = 2.\]
So the maximum point on the graph of \(f(x) = \dfrac{2}{\sqrt{1 + (x-1.5)^2}}\) occurs at coordinates \((1.5, 2)\) and the functions on the two cards have the same maximum value.
Looking at the combined graph, it is clear that the area under the function on card (b), \(f(x) = \dfrac{2}{\sqrt{1 + (x-1.5)^2}}\), is greater than that on card (a), \(f(x) = (4 - x^2)^{\frac{1}{2}}\), between \(x=1\) and \(x=2\).
We can also say that the area on card (b) is less than double that on card (a).
Can we be any more specific about the proportion of the area on card (b) taken up by the area on card (a)?
With the function on this card we can calculate the required area exactly.
We can exploit the fact that we know we are looking at a semi-circle. In the diagram below we can see that the green sector is made up of the purple area that we want plus a right-angled triangle (of base length \(1\) and hypotenuse length \(2\)).
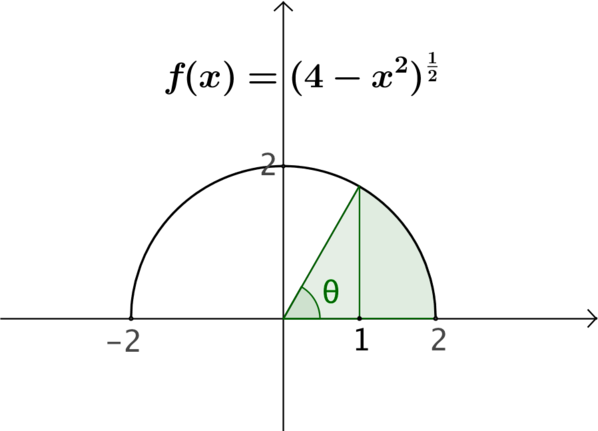
We can therefore obtain the required area by first calculating of the green sector and then subtracting the area of the triangle.
Calculating the area of the sector
In order to calculate the area of the sector we need to know what proportion it is of the original semi-circle. We can deduce this from the value of the angle \(\theta\).
By applying trionometry to the right-angled triangle we find that \[\theta = \arccos\left(\frac{1}{2}\right) = \frac{\pi}{3}.\]
This means that the green sector is exactly \(\dfrac{1}{3}\) of the area of the semi-circle, and therefore has an area of \(\dfrac{2\pi}{3}\).
We have chosen to express the angle \(\theta\) in radians.
We could just have easily used degrees with the same result:
\[\theta = \arccos{\left(\frac{1}{2}\right)} = \frac{\pi}{3} \textrm { radians} \ \textrm {or} \ 60^{\circ}.\]
Calculating the area of the triangle
We know that the base length of the triangle is \(1\) and that its hypotenuse is of length \(2\). There are now two ways in which we could determine its vertical height: we could directly apply Pythagoras’ Theorem, or we could find the value of \(f(1)\).
Using either approach, the height of the triangle is found to be \(\sqrt{3}\). Therefore the area of the triangle will be \(\dfrac{\sqrt{3}}{2}\).
Calculating the original purple area
The area under the curve between \(x=1\) and \(x=2\) can now be calculated as \[\frac{2\pi}{3} - \frac{\sqrt{3}}{2} = \frac{4\pi - 3\sqrt{3}}{6} \approx 1.23.\]
The approximate decimal value may useful when we come to compare this area to that on card (b).
We do not yet have any techniques for finding an exact value for this area. We can however find an approximation for the area that will allow us to answer the question posed in this problem.
The function shown on this card is a horizontal translation of the function \(g(x) = \dfrac{2}{\sqrt{1+x^2}}\) and will therefore have the same area as \(g(x)\) between \(x=-0.5\) and \(x=0.5\).
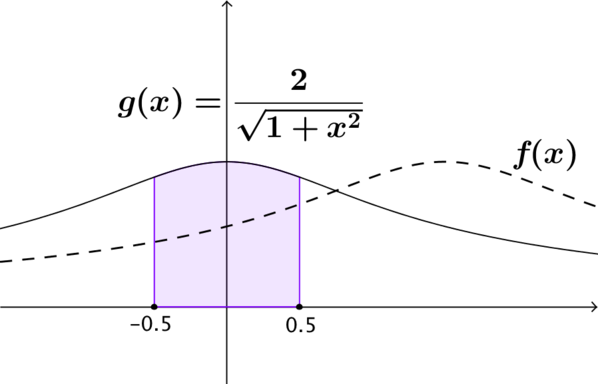
We can show that \(g(x) = g(-x)\) and hence that \(g(x)\) is an even function. This in turn means that \(g(x)\) is symmetrical about \(x=0\) (and that \(f(x)\) is symmetrical about \(x=1.5\)).
Exploiting the symmetry properties of this function will reduce the amount of work we need to do to obtain an approximate value for the area that is ‘good enough’ for this problem.
It now doesn’t matter whether we return to the original function, \(f(x)\), or follow through our working with the translated function, \(g(x)\), (we have already observed that the areas are equivalent as long as we look at the translated region). If we choose to work with \(g(x)\), we need to consider a method of approximating the area under \(g(x)\) between \(x=0\) and \(x=0.5\) (doubling this value will then give us an estimate for the whole area between \(x=-0.5\) and \(x=0.5\)).
We might choose to use a single trapezium to do this in the first instance, giving us a lower bound for the area.

In this case we can write \[\textrm{Area (b)} \approx \frac{1}{2} \left[g(0) + g\left(\frac{1}{2}\right)\right] = \frac{1}{2}\left[2 + \frac{4}{\sqrt{5}}\right] \approx 1.89.\]
Now, we can see that this is an under-estimate of the area and so we can say \[\textrm{Area (b)} > 1.89.\]
We might have chosen to use the trapezium rule, dividing the area into two trapezia, each of width \(0.25\) (or \(\tfrac{1}{4}\)) giving
\[\textrm{Area (b)} \approx \frac{1}{4}\left[g(0) + 2 g\left(\frac{1}{4}\right) + g\left(\frac{1}{2}\right)\right] = \frac{1}{4} \left[2 + \frac{16}{\sqrt{17}} + \frac{4}{\sqrt{5}} \right] \approx 1.92.\]
Using software such as GeoGebra to compute the area we find that our approximate value is actually correct to two decimal places. This level of accuracy was achieved by completing calculations for just two trapezia, the equivalent of dividing the total area into four trapezia.
Can this level of accuracy be guaranteed when using the trapezium rule, with four trapezia, to estimate areas under other functions?
What is it about this function that makes the trapezium rule such a good fit?
What can we say now about the proportion of the area on card (b) taken up by the area on card(a)?

