Consider this situation, where one edge of the rectangle lies on the line \(AB\).

How does your approach to each situation compare?
How does the area of the rectangle identified in each situation compare?
It would seem sensible to attempt to approach this using methods similar to those used in the first problem.
As before, one of the first things needed in an algebraic approach is to identify the length of the rectangle that lies on the line \(AB\) in terms of \(y\) and the side lengths of the triangle \(a\), \(b\), \(c\).
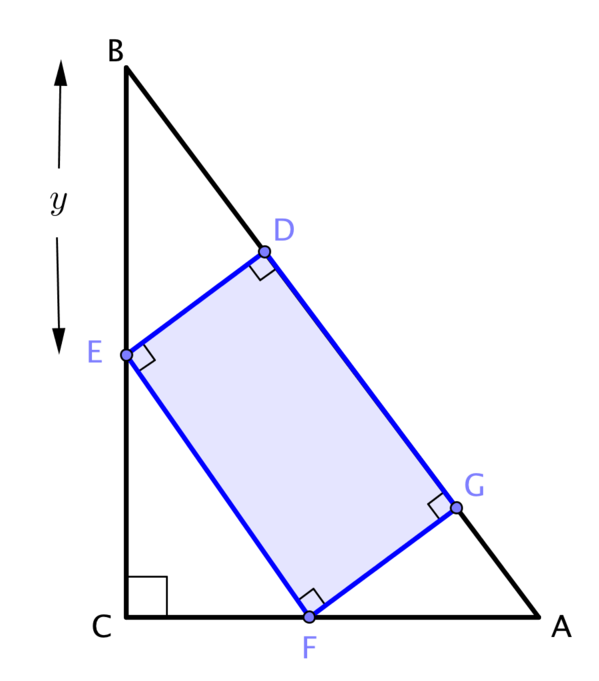
As before, one of the first things we must do is decide which length in the diagram to consider as our variable. In the original scenario it seemed sensible to select one of the sides of the rectangle to vary.
So which will be the best choice of variable this time? Why might we choose to label length \(y\)?
In the previous situation I used similar triangles to identify the missing lengths. By considering the interior angles of each of the smaller white triangles (\(GFA\), \(CEF\), and \(BDE\)) I can show that all are in fact similar to triangle \(ABC\).
If I now consider triangle \(DBE\) I can calculate the linear scale factor from this to triangle \(ABC\) as \[\frac{BE}{BA} = \frac{y}{c}\] and therefore the length \(ED=\dfrac{by}{c}\).
Now I consider triangle \(FEC\). Length \(EC=a-y\) and so the linear scale factor from this triangle to triangle \(ABC\) is given by \[\frac{EC}{BC} = \frac{a-y}{a}.\] Length \(EF\) can now be written as \(\dfrac{c(a-y)}{a}\).
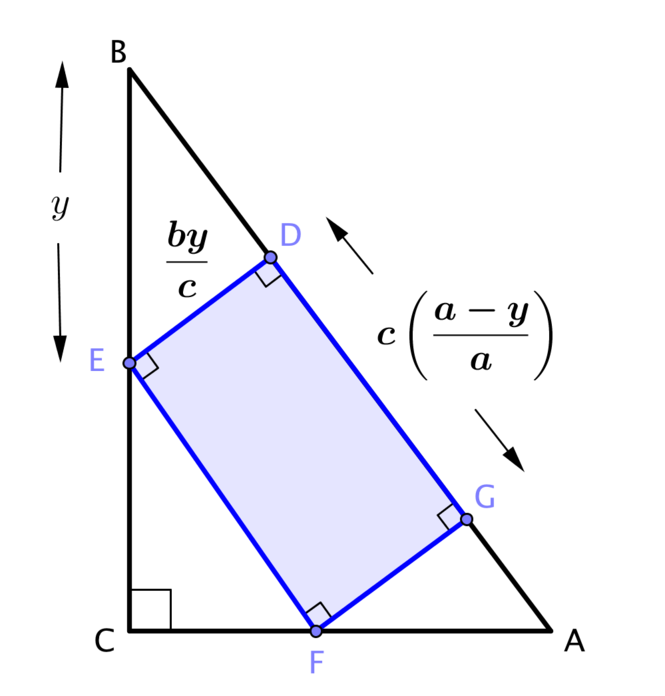
The area of the blue rectangle can now be expressed as \[\left(\frac{by}{c}\right)\left(\frac{c(a-y)}{a}\right) = \frac{by(a-y)}{a} = \left(\frac{b}{a}\right)(ay-y^2).\]
Once again I am dealing with a quadratic equation that has a maximum point that can be located by sketching the graph.

The maximum value occurs when \(y=\dfrac{a}{2}\) which corresponds to a maximum area of \(\dfrac{ab}{4}\).
Notice that once again it is the case that if a rectangle is inscribed inside a right-angled triangle in this way, its greatest area will be exactly half that of the triangle.
The algebraic approach is not the only valid method. Often we use algebra as part of our first attempt to solve a problem, but it may be beneficial to think about other approaches first. We can also consider a geometric approach here. Can you construct a similar folding argument to the one that was used in the first problem?

