Review question R7119 at the Combining Functions station
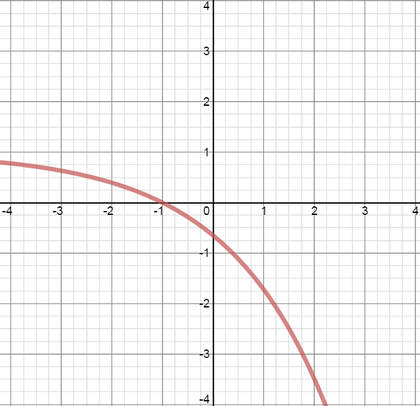
The diagram below shows the graph of the function \(y = f(x)\).
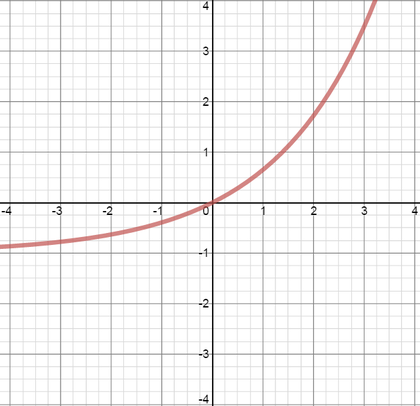
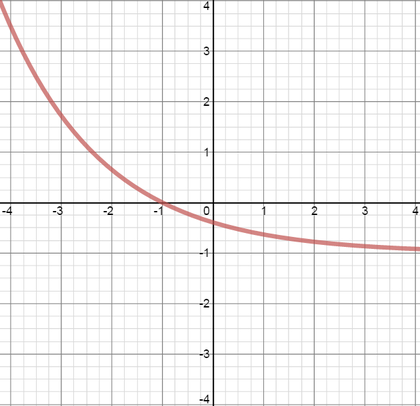
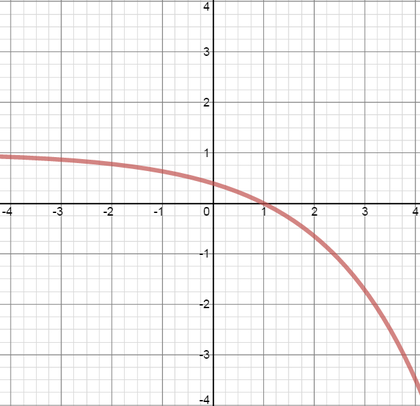
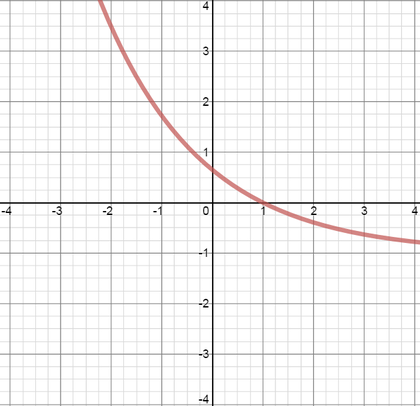
The graph of the function \(y = -f(x+1)\) is drawn in which of the following diagrams?
|
|
|
|
|
|
Using this Review question
This relatively short problem invites students to review their understanding of function transformations. It could also be used to support a developing understanding of this concept and then later revisited to review the ideas.
An extension problem is to work out the equations of the other three graphs in terms of \(f(x)\), and then to explain why. Alternatively, the problem could also be turned into a matching activity: students could be given the four equations \(y=-f(x+1)\), \(y=-f(x-1)\), \(y=f(-x+1)\) and \(y=f(-x-1)\), and then asked to match them to the graphs.
It would be valuable for the students to then check their answers using graphing software such as Desmos or GeoGebra, as they are very likely to get the last two the wrong way round. Students could also be challenged to find a suitable function \(f(x)\) for their explorations, or could be given a function such as \(f(x)=1.6^x-1\) to work with. Both of these graphing systems allow functions to be defined and used by entering something like “\(f(x)=1.6^x-1\)” and then “\(y=-f(x)\)”.
This extension and checking activity can then be used as a stimulus to develop a deeper understanding of the mathematics involved.
Some further suggestions
During the Tying it together webinar, participants suggested other questions that could be asked either about this problem or stimulated by it, including:
What transformations do the other sketches represent?
What sketch would we have had to start with for the other answers to be correct?
How do you transform the one you have identified to another of the graphs?
Can you make up another question like this?
Can you sketch the graphs of \(y=\dfrac{1}{x}+1\) and \(y=\dfrac{1}{x+1}\)?
Aspects of mathematical thinking
Mathematical behaviours to look out for
Using a specific value of \(x\) to eliminate or test possibilities
With the extension in particular, testing ideas, and asking themselves what has gone wrong if the software gives a different answer from their prediction.
Overarching ideas
Pervasive idea: Transforming
Justifying and convincing
Common issues and misconceptions
Confusing the effects of different graph transformations by relying on memorising
With the extension, thinking that \(y=f(-x-1)\) means “reflect, then translate by \(1\) to the right”
Some related resources
- Transformers
- R9673
- Rich resources and Review questions on other aspects of composition of functions can be found at the Combining Functions station